library(tidyverse)Module 7: Correlation and Regression
- The main goal of this lesson is to understand, conduct, and interpret both correlation and regression analyses. We will examine Pearson’s \(r\) correlation coefficient and learn how to conduct and interpret an inferential statistical test using this common statistic. Additionally, we will explore regression models and their components, including computing the slope and intercept for simple linear regression and the multiple slopes and intercept for multiple linear regression. Finally, we will learn how to interpret the regression output from R, tying together these key analytical techniques.
At a Glance
- In order to succeed at this lesson, you will use a statistical model, called linear regression, that helps us understand an outcome variable and also allows us to make predictions for future instances, or the next occurrence. A linear regression model is quite commonly used in many fields and is often the foundation for future more advanced analysis like machine learning. Linear regression can be a fairly easy way to design and test a research model, and in doing so allows us to gauge helpful predictor variables in understanding a phenomenon. Not only can we understand a research model, but we can also make stronger predictions on the future.
Lesson Objectives
- Compute and interpret Pearson’s r correlation coefficient.
- Conduct an inferential statistical test for Pearson’s r correlation coefficient.
- Explore the statistical model for a line.
- Compute the slope and intercept in a simple linear regression.
- Interpret a regression model significance and model fit.
Consider While Reading
- In this lesson, we will focus on inference for correlation and regression analysis, learning how to conduct a correlation test as well as single and multiple linear regression tests. This builds on the scatterplots introduced in the Data Visualization lesson, which help us visually describe relationships between variables. By revisiting those concepts, we will explore how visualizations can aid in making inferences alongside regression and correlation results. Additionally, we will differentiate between ANOVA, which examines differences between means in categorical data, and linear regression, which focuses on estimating responses or predictions while forming a regression line.
Correlation
Covariance
- Covariance (\(s_{xy}\) or \(cov_{xy}\)) is a numerical measure that describes the direction of the linear relationship between two variables, x and y and reveals the direction of that linear relationship.
- The formula for covariance is as follows:
- \(cov_{xy} = \sum^n_{i=1}(x_i-m_x)*(y_i-m_y)/(n-1)\)
- Where \(x_i\) and \(y_i\) are the observed values for each observation, \(m_x\) and \(m_y\) are the mean values for each variable, \(i\) represents an individual observation, and \(n\) represents the sample size.
x <- c(3, 8, 5, 2)
y <- c(12, 14, 8, 4)
devX <- x - mean(x)
devY <- y - mean(y)
covXY <- sum(devX * devY)/(length(x) - 1)
covXY[1] 8.333333# We can verify this by using cov() function in R.
cov(x, y)[1] 8.333333Correlation Coefficient
- A correlation coefficient (\(r_{xy}\)) describes both the direction and strength of the relationship between \(x\) and \(y\). \(r_{xy} = cov_{sy}/(s_xs_y)\) or using the standardized formula in the book:
- \(r_{xy} = \sum^n_{i=1}(z_x*z_y)/(n-1)\)
# Calculated manually
covXY/(sd(x) * sd(y))[1] 0.7102387# We can verify this by using cor() function in R.
cor(x, y)[1] 0.7102387Rules for the Correlation Coefficient
- The correlation coefficient has the same sign as the covariance; however, its value ranges between −1 and +1 whereas \(-1 \le r_{xy} \le +1\).
- The absolute value of the coefficient reflects the strength of the correlation. So a correlation of −.70 is stronger than a correlation of +.50.

Interpreting the Direction of the Correlation
- Negative correlations occur when one variable goes up and the other goes down.
- No correlation happens when there is no discernible pattern in how two variables vary.
- Positive correlations occur when one variable goes up, and the other one also goes up (or when one goes down, the other one does too); both variables move together in the same direction.

Scatterplots to Visualize Relationship
Let’s do an example to first visualize the data, and then to calculate the correlation coefficient.
First, read in a .csv called DebtPayments.csv. This data set has 26 observations and 4 variables:
- A character variable with a bunch of metropolitan areas listed;
- An integer numeric debt;
- A numeric variable Income;
- A numeric variable Unemployment.
Debt_Payments <- read.csv("data/DebtPayments.csv")
str(Debt_Payments)'data.frame': 26 obs. of 4 variables:
$ Metropolitan.area: chr "Washington, D.C." "Seattle" "Baltimore" "Boston" ...
$ Debt : int 1285 1135 1133 1133 1104 1098 1076 1045 1024 1017 ...
$ Income : num 103.5 81.7 82.2 89.5 75.9 ...
$ Unemployment : num 6.3 8.5 8.1 7.6 8.1 9.3 10.6 12.4 12.9 9.7 ...Next, plot the relationship between 2 continuous variables.
- There are a few ways to write the plot command using ggplot. We went over these in the Data Visualization lesson. Again we said:
- Layer 1: ggplot() command with aes() command directly inside of it pointing to x and y variables.
- Layer 2: geom_point() command to add the observations as indicators in the chart.
- Layer 3 or more: many other optional additions like labs() command (for labels) or stat_smooth() command to generate a regression line.
Debt_Payments %>% ggplot(aes(Income, Debt)) + geom_point(color = "#183028", shape = 2) + stat_smooth(method = "lm", color = "#789F90") + theme_minimal()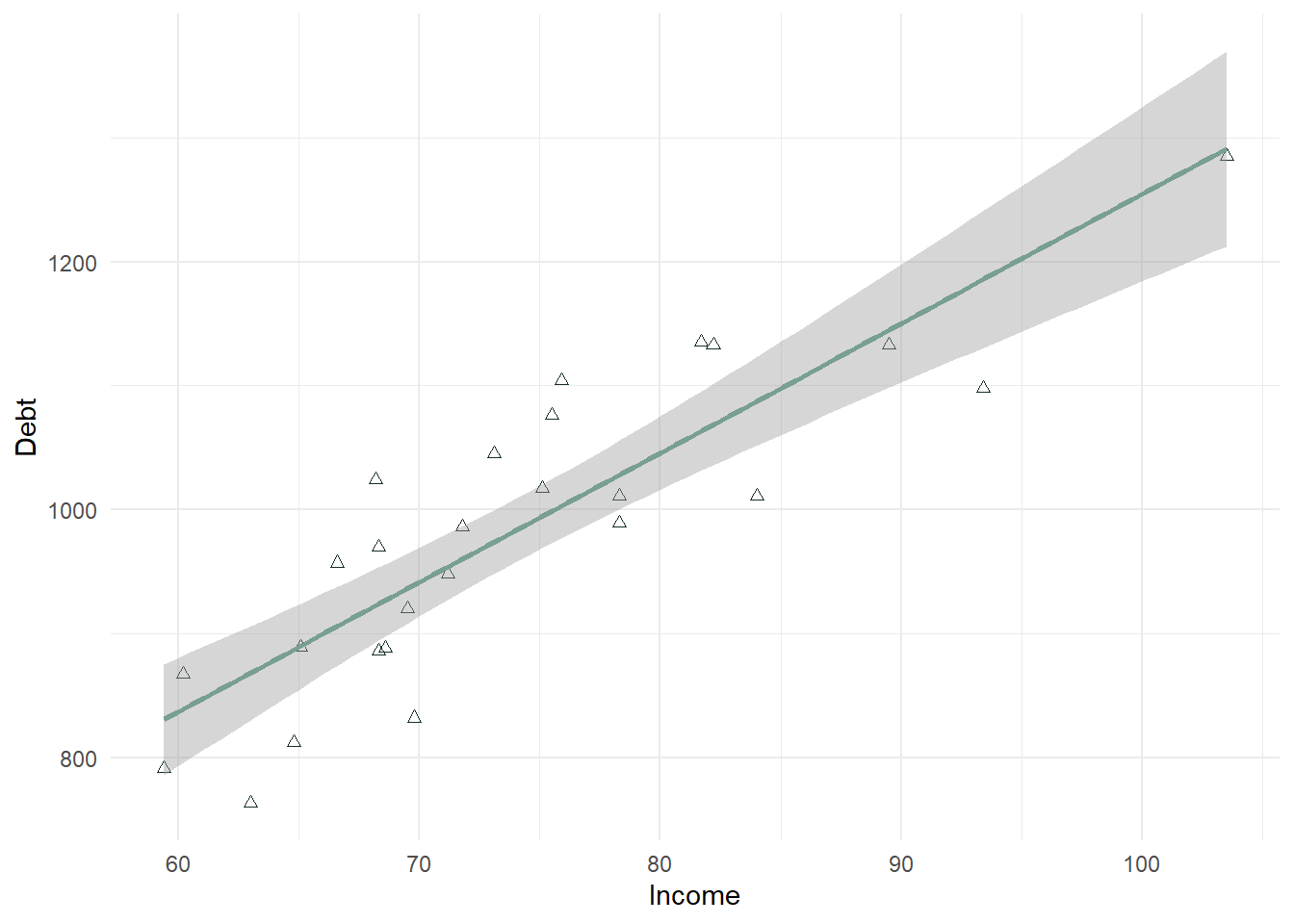
In the above plot, there is a strong positive relationship (upward trend) that should be confirmed with a correlation test.
In a second example below, we look at Unemployment as the X variable. This scatterplot is much more difficult to use in determining whether the correlation will be significant. It looks negative, but there is not a strong linear trend to the data. This will also need to be confirmed with a correlation test.
Debt_Payments %>%
ggplot(aes(Unemployment, Debt)) + geom_point(color = "#183028", shape = 2) +
stat_smooth(method = "lm", color = "#789F90") + theme_minimal()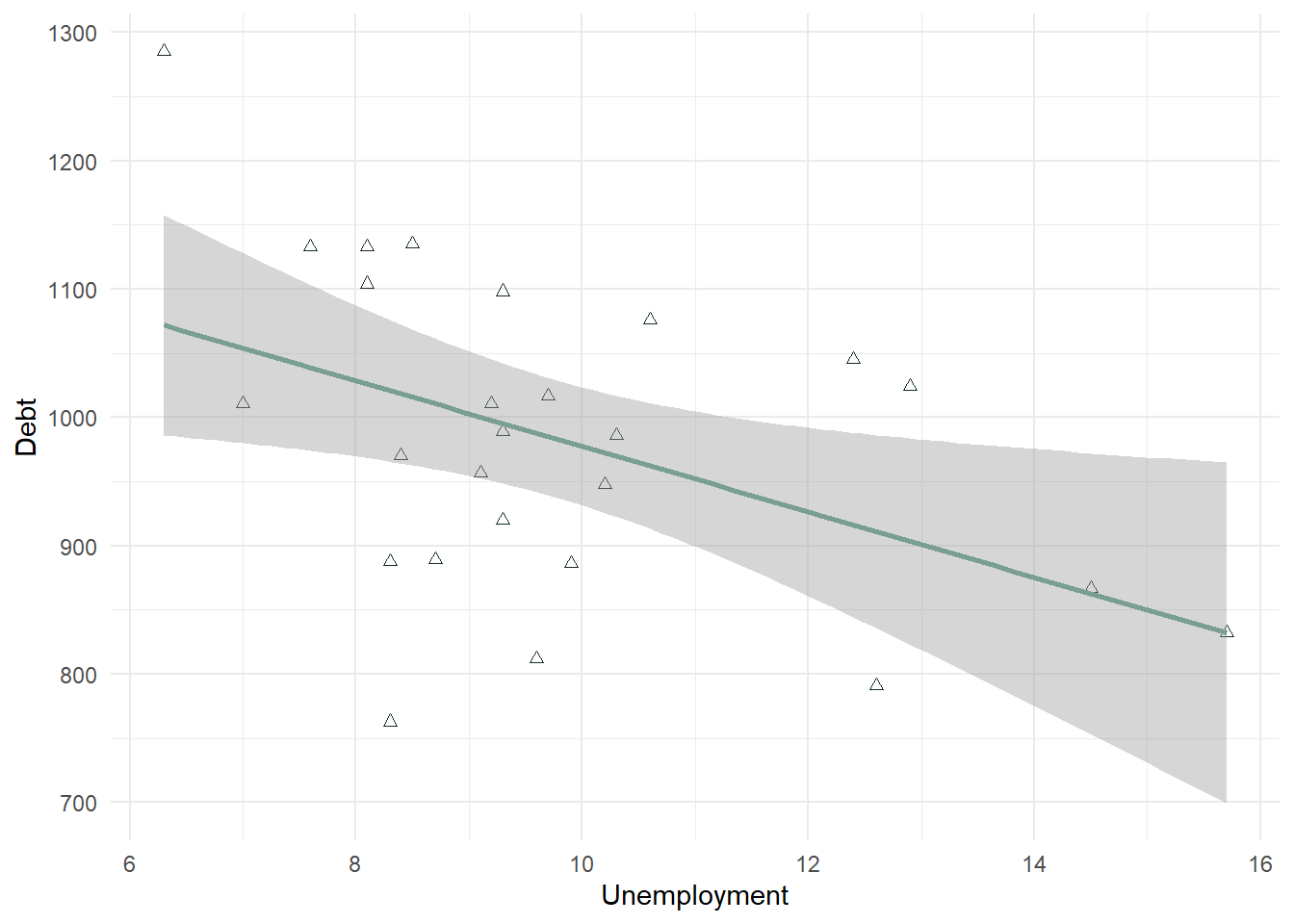
- In many scatterplots using big data, the observations are too numerous to see a good relationship. In that case, the statistical test can trump this visual aid. However, in a lot of cases the scatterplot does help visualize the relationship between 2 continuous variables.
Interpreting the Strength of the Correlation
- Statisticians differ on what is called a strong correlation versus weak correlation, and it depends on the context. A .9 may be required for a strong correlation in one field, and a .5 in another. Generally speaking in business, the absolute value of a correlation .8 or above is considered strong, between .5 and .8 is considered moderate, and between a .2 and .5 is considered weak.
- The following is consistent with what is most generally used:

Interpreting the Significance of the Correlation
- Correlation values should be tested alongside a p-value to confirm whether or not there is a correlation. The null is tested using a t-distribution specifically testing whether \(r = 0\) or not, like the one-sample t-test section from the lesson 6.
- The null and alternative are listed below.
- \(H_0\): There is no relationship between the two variables (\(r = 0\)).
- \(H_A\): There is a relationship between the two variables (\(r \neq 0\)).
- Even small correlations can be significant: In large datasets, even a small correlation, like .1, can be statistically significant due to the increased power that comes with a high sample size. It’s important to interpret both the strength of the correlation and its practical significance in context.
Statistical significance answers the question: “Is the effect real?“
Statistical Significance:
A result is statistically significant if it is unlikely to have occurred by random chance, given a pre-defined threshold (usually p < 0.05).
With larger sample sizes, even very small effects can become statistically significant because larger samples reduce variability. For example, a correlation of 0.1 can be statistically significant with enough data.
Practical Significance:
Practical significance answers the question: “Is the effect meaningful?“
Practical significance refers to the real-world importance or relevance of a result. It asks, “Does this effect matter in practice?“
Even if a result is statistically significant, it may not be large enough to have a meaningful impact on business decisions or outcomes.
cor.test() Command
- The cor() command gives you just the correlation coefficient. This command can be useful if you are testing many correlations at one time. In the below statement, I can use \(cor(Variable1, Variable2)\) to see the correlation between 2 continuous variables.
cor(Debt_Payments$Income, Debt_Payments$Debt)[1] 0.8675115- The cor.test() command tests the hypothesis whether \(r=0\) or not. This command comes with a p-value and t-test statistic (along with the correlation coefficient).
cor.test(Debt_Payments$Income, Debt_Payments$Debt)
Pearson's product-moment correlation
data: Debt_Payments$Income and Debt_Payments$Debt
t = 8.544, df = 24, p-value = 9.66e-09
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.7231671 0.9392464
sample estimates:
cor
0.8675115 - This test shows a strong positive correlation of .8675 (>.8) which is significant. Our p-value is 9.66e-09 or < .001 alpha level. This suggests that we reject the null hypothesis and support the alternative that \(r \neq 0\) which confirms a correlation is present.
- We also see a confidence interval listed. It suggests that we are 95% confident that the correlation is between .723 and .939.
cor.test(Debt_Payments$Income, Debt_Payments$Unemployment)
Pearson's product-moment correlation
data: Debt_Payments$Income and Debt_Payments$Unemployment
t = -3.0965, df = 24, p-value = 0.004928
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.7636089 -0.1852883
sample estimates:
cor
-0.5342931 - This test shows a moderate negative correlation of -.534 (<.5 and .8) which is significant. Our p-value is 0.004928 or < .01 alpha level. This suggests that we reject the null hypothesis and support the alternative that \(r \neq 0\) which confirms a correlation is present.
- We also see a confidence interval listed. It suggests that we are 95% confident that the correlation is between -.765 and -.185. This confidence interval is wider than the one listed above. This is due to the noise in the relationship we noted in the scatterplot - the correlation is weaker, the relationship does not look as linear, the confidence decreases. Even though this is true, we must note that we still found a significant correlation.
Additional Examples
library(ISLR)
data("Credit")
summary(Credit) ID Income Limit Rating
Min. : 1.0 Min. : 10.35 Min. : 855 Min. : 93.0
1st Qu.:100.8 1st Qu.: 21.01 1st Qu.: 3088 1st Qu.:247.2
Median :200.5 Median : 33.12 Median : 4622 Median :344.0
Mean :200.5 Mean : 45.22 Mean : 4736 Mean :354.9
3rd Qu.:300.2 3rd Qu.: 57.47 3rd Qu.: 5873 3rd Qu.:437.2
Max. :400.0 Max. :186.63 Max. :13913 Max. :982.0
Cards Age Education Gender Student
Min. :1.000 Min. :23.00 Min. : 5.00 Male :193 No :360
1st Qu.:2.000 1st Qu.:41.75 1st Qu.:11.00 Female:207 Yes: 40
Median :3.000 Median :56.00 Median :14.00
Mean :2.958 Mean :55.67 Mean :13.45
3rd Qu.:4.000 3rd Qu.:70.00 3rd Qu.:16.00
Max. :9.000 Max. :98.00 Max. :20.00
Married Ethnicity Balance
No :155 African American: 99 Min. : 0.00
Yes:245 Asian :102 1st Qu.: 68.75
Caucasian :199 Median : 459.50
Mean : 520.01
3rd Qu.: 863.00
Max. :1999.00 attach(Credit)
cor.test(Rating, Income) #0.7913776 moderate and positive
Pearson's product-moment correlation
data: Rating and Income
t = 25.826, df = 398, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.751651 0.825383
sample estimates:
cor
0.7913776 cor.test(Rating, Balance) #0.8636252 strong and positive
Pearson's product-moment correlation
data: Rating and Balance
t = 34.176, df = 398, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.8363997 0.8865997
sample estimates:
cor
0.8636252 cor.test(Rating, Limit) #0.9968797 strong and positive
Pearson's product-moment correlation
data: Rating and Limit
t = 251.95, df = 398, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.9962026 0.9974363
sample estimates:
cor
0.9968797 ## almost perfectly linear
ggplot(Credit, aes(Rating, Limit)) + geom_point()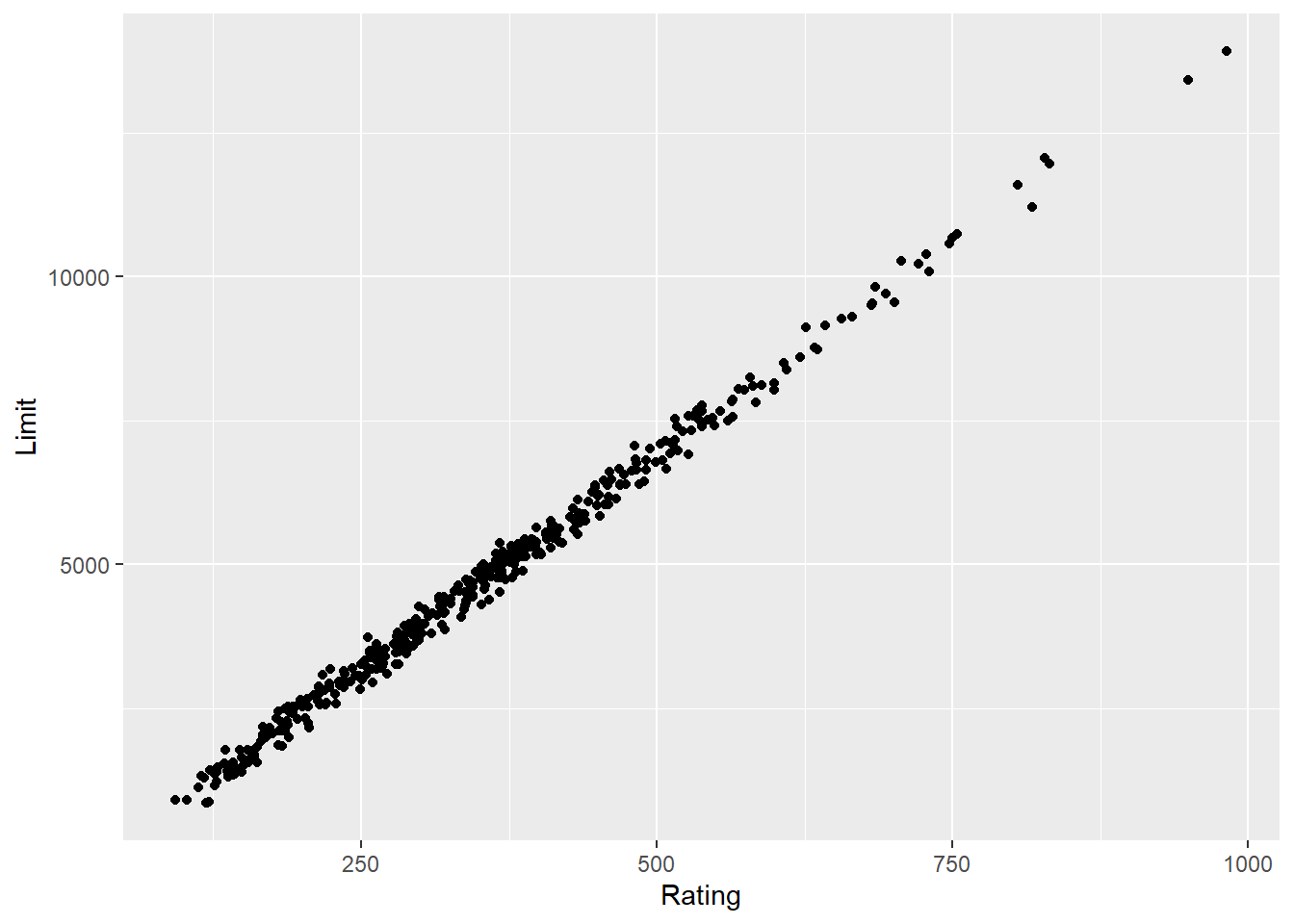
cor.test(Rating, Education) #-0.03013563 no correlation
Pearson's product-moment correlation
data: Rating and Education
t = -0.60148, df = 398, p-value = 0.5479
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.12780969 0.06811737
sample estimates:
cor
-0.03013563 cor.test(Rating, Age) #0.103165 - between -.2 and .2 - so no relationship even though p-value < .05 -- p-value fails at .01 level.
Pearson's product-moment correlation
data: Rating and Age
t = 2.0692, df = 398, p-value = 0.03917
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.005165528 0.199201690
sample estimates:
cor
0.103165 ggplot(Credit, aes(Rating, Age)) + geom_point() + stat_smooth(method = "lm")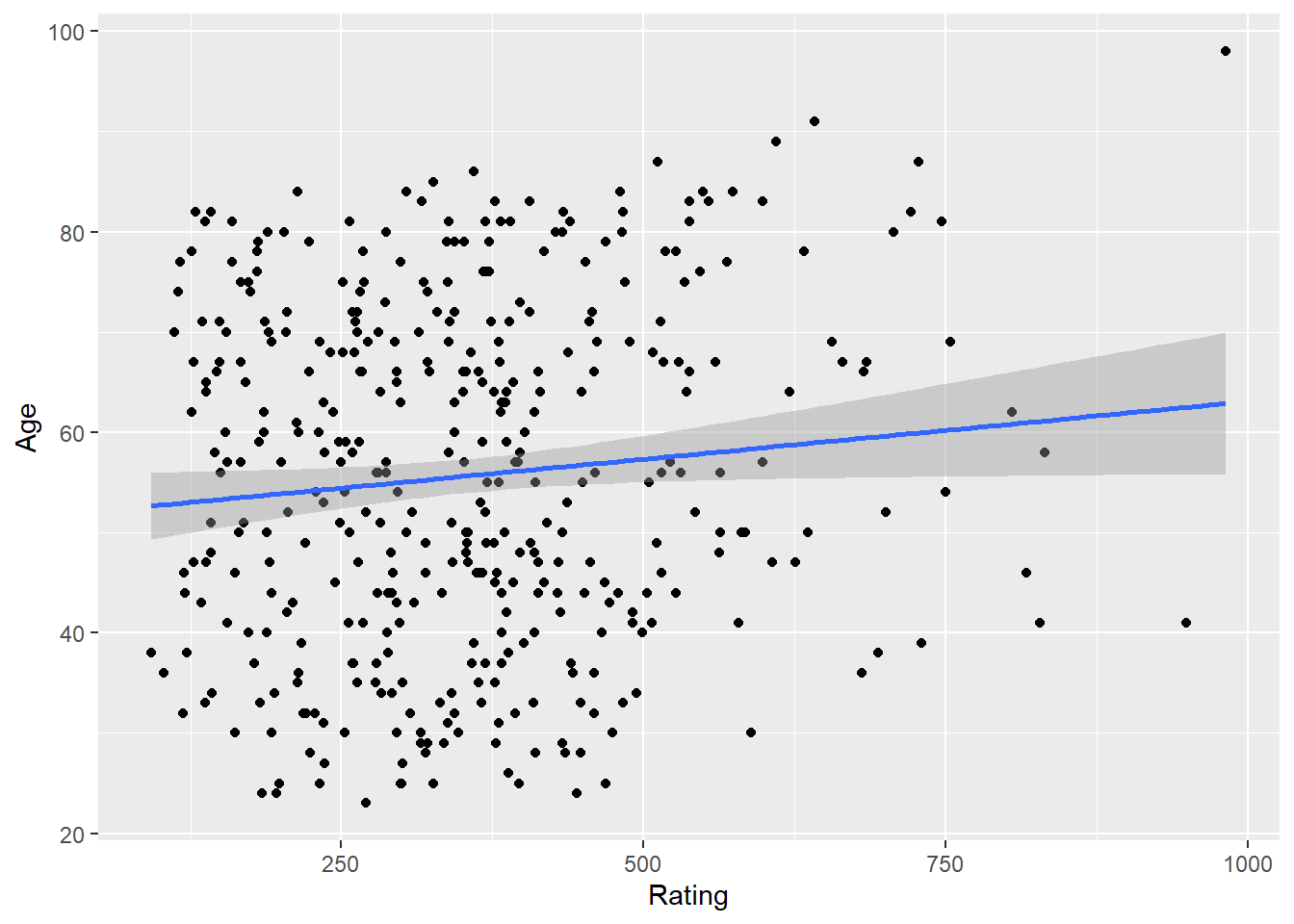
cor.test(Rating, Cards) #0.05323903
Pearson's product-moment correlation
data: Rating and Cards
t = 1.0636, df = 398, p-value = 0.2881
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.04504785 0.15050509
sample estimates:
cor
0.05323903 ggplot(Credit, aes(Rating, Cards)) + geom_point() + stat_smooth(method = "lm")
Comparing to t.test and ANOVA
- A t-test examines if there is a significant difference in the means of two groups on a dependent variable. For example, whether males and females differ in their credit ratings, where a correlation measures the strength and direction of a linear relationship between two continuous variables, such as Rating and Income.
- An independent t-test requires a categorical independent variable (e.g., Gender) with two levels and a continuous dependent variable (e.g., Rating), where a correlation requires two continuous variables.
- Both can provide insights into relationships in the dataset, but they address different questions. An independent t-test evaluates mean differences (group comparisons), while correlation evaluates relationships (continuous covariation). * A significant t-test does not imply a strong correlation between the grouping variable and the dependent variable; the correlation would depend on the coding of the categorical variable and the distribution of data
## -- Example of an independent t.test using same dataset
t.test(Rating ~ Gender, data = Credit) ##no group differences
Welch Two Sample t-test
data: Rating by Gender
t = -0.17703, df = 393.54, p-value = 0.8596
alternative hypothesis: true difference in means between group Male and group Female is not equal to 0
95 percent confidence interval:
-33.26095 27.76582
sample estimates:
mean in group Male mean in group Female
353.5181 356.2657 ggplot(Credit, aes(Gender, Rating)) + geom_boxplot()
t.test(Rating ~ Married, data = Credit) ##no group differences
Welch Two Sample t-test
data: Rating by Married
t = -0.74241, df = 340.4, p-value = 0.4584
alternative hypothesis: true difference in means between group No and group Yes is not equal to 0
95 percent confidence interval:
-42.54190 19.22762
sample estimates:
mean in group No mean in group Yes
347.8000 359.4571 ggplot(Credit, aes(Married, Rating)) + geom_boxplot()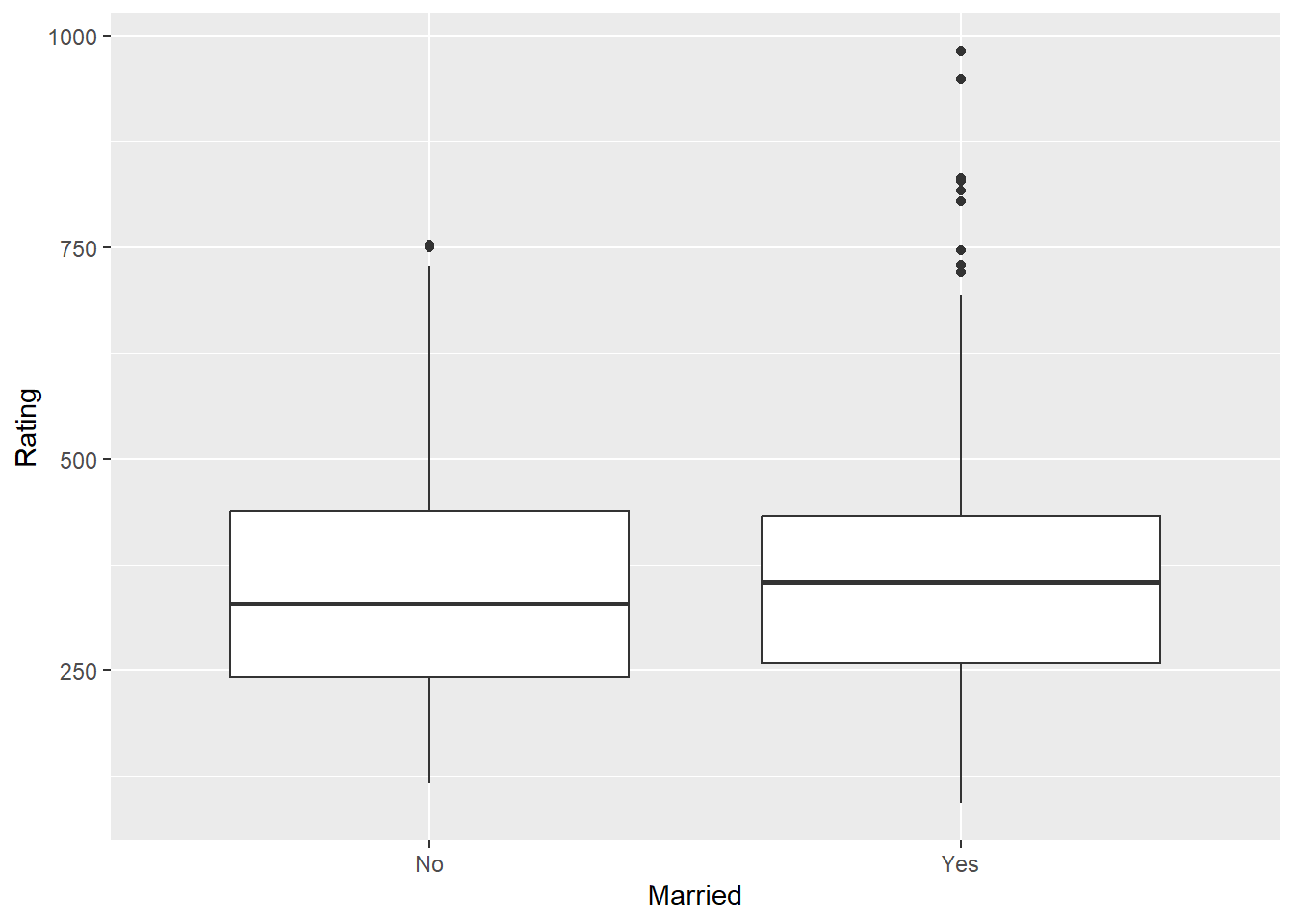
- An ANOVA tests for significant differences in the means of three or more groups on a dependent variable. For example, whether credit ratings differ across ethnic groups, where a correlation examines the strength of the relationship between two continuous variables.
- An Anova requires a categorical independent variable (with three or more levels) and a continuous dependent variable, where a correlation requires two continuous variables.
- ANOVA focuses on group comparisons (e.g., Rating differences across Ethnicity), while correlation looks at how two variables change together.A significant ANOVA could suggest that the categorical grouping variable explains some variance in the dependent variable, but this variance is not quantified as a relationship strength (as correlation would provide).
## -- Example of An ANOVA using same dataset
anova1 <- aov(Rating ~ Ethnicity, data = Credit)
anova(anova1) #no group differences - no need for a post hoc test. Analysis of Variance Table
Response: Rating
Df Sum Sq Mean Sq F value Pr(>F)
Ethnicity 2 19388 9694.1 0.4037 0.6681
Residuals 397 9532496 24011.3 ggplot(Credit, aes(Ethnicity, Rating, fill = Ethnicity)) + geom_boxplot(show.legend = FALSE)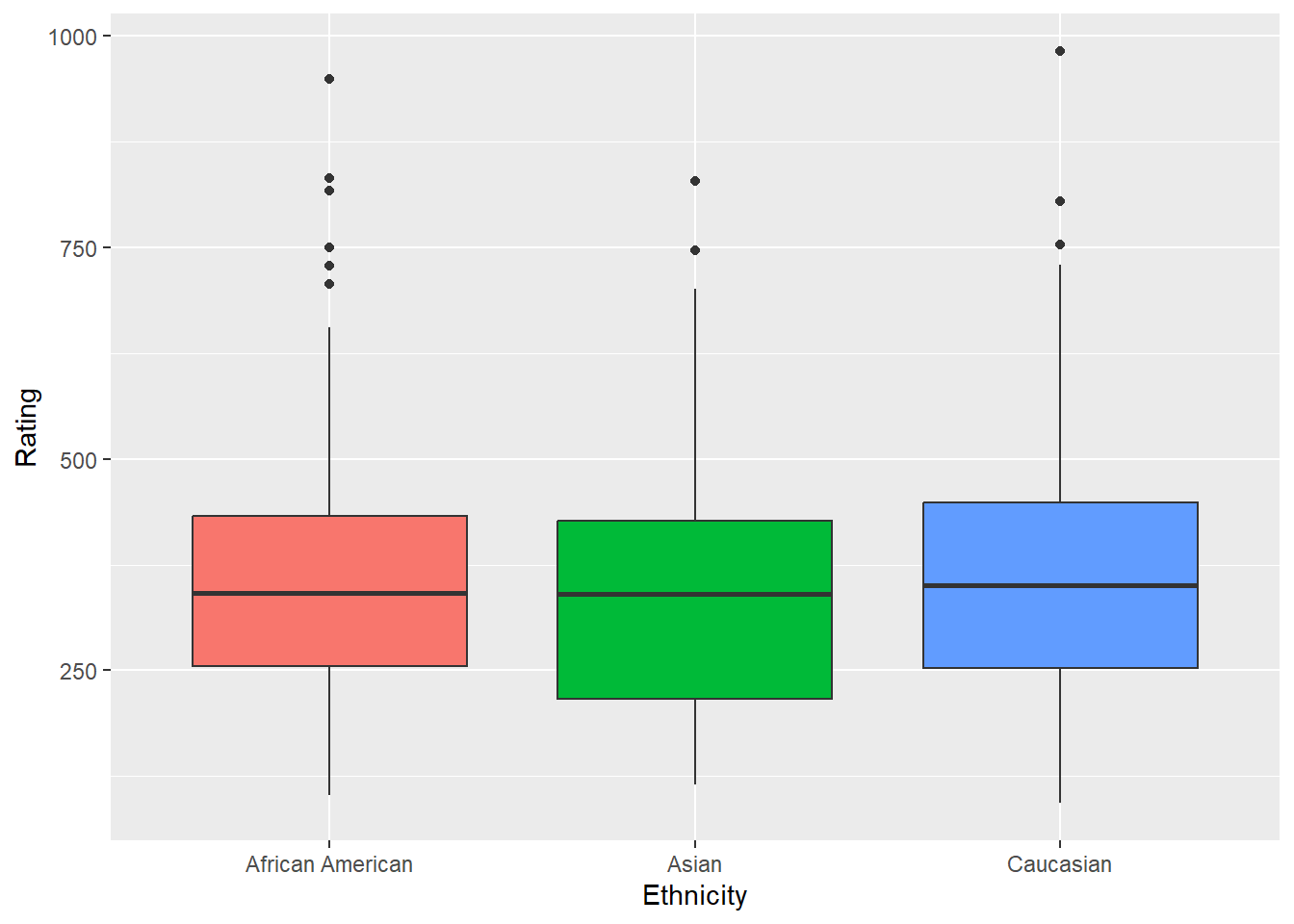
Limitations of Correlation Analysis
Note that a correlation is the first step in understanding causality. Correlation and causality are closely related but fundamentally different concepts in data analysis. Correlation refers to the statistical relationship between two variables, indicating how changes in one variable are associated with changes in another. However, it does not imply that one variable causes the other to change. Causality, on the other hand, goes beyond mere association to establish a cause-and-effect relationship, where one variable directly influences the other. Determining causality requires meeting specific criteria, including significant association, temporal precedence (the cause precedes the effect), and ruling out alternative explanations or confounding variables. While correlation is often the first step in exploring potential relationships, additional analysis—such as experimental design or causal modeling—is necessary to confirm causality. This distinction highlights the importance of critical thinking when interpreting statistical results, as a strong correlation alone does not prove that one variable is the cause of another.
To determine a causal model, you need the following:
- Significant Correlation: Statistically significant relationship between the variables.
- Temporal Precedence: Causal variable occurred prior to the other variable.
- Eliminate Alternate Variables: No other factors can account for the cause.
- Some limitations are as follows:
- The correlation coefficient captures only a linear relationship.
- The correlation coefficient may not be a reliable measure in the presence of outliers.
- Even if two variables are highly correlated, one does not necessarily cause the other.
- When interpreting results, note that lack of significance does not mean a variable X has no relationship with Y; it might suggest a more complex or non-linear relationship.
The Linear Regression Model
Overview of the Linear Regression
- Linear regression analysis is a predictive modelling technique used for building mathematical and statistical models that characterize relationships between a dependent (continuous) variable and one or more independent, or explanatory variables (continuous or categorical), all of which are numerical.
- This technique is useful in forecasting, time series modelling, and finding the causal effect between variables.
- Simple linear regression involves one explanatory variable and one response variable.
- Explanatory variable: The variable used to explain the dependent variable, usually denoted by X. Also known as an independent variable or a predictor variable.
- Response variable: The variable we wish to explain, usually denoted by Y. Also known as a dependent variable or outcome variable.
- Multiple linear regression involves two or more explanatory variables, while still only one response variable.
Examples of Independent and Dependent Variables
- Example Question: Does increasing the marketing budget lead to higher sales revenue?
- Independent Variable: Marketing budget (how much money is spent on advertising and promotions).
- Dependent Variable: Sales revenue (how much income the business generates from sales).
- Example Question: Does additional training improve employee productivity?
- Independent Variable: Hours of employee training.
- Dependent Variable: Employee productivity (e.g., units produced per hour or sales closed per month).
- Example Question: Does being a member of a loyalty program increase the frequency of repeat purchases?
- Independent Variable: Participation in a loyalty program (whether a customer is a member or not).
- Dependent Variable: Number of repeat purchases by the customer.
Estimating Using a Simple Linear Regression Model
- While the correlation coefficient may establish a linear relationship, it does not suggest that one variable causes the other.
- With regression analysis, we explicitly assume that the response variable is influenced by other explanatory variables.
- Using regression analysis, we may predict the response variable given values for our explanatory variables.
Inexact Relationships
- If the value of the response variable is uniquely determined by the values of the explanatory variables, we say that the relationship is deterministic.
- But if, as we find in most fields of research, that the relationship is inexact due to omission of relevant factors, we say that the relationship is inexact.
- In regression analysis, we include a stochastic error term, that acknowledges that the actual relationship between the response and explanatory variables is not deterministic.
Regression as ANOVA
- ANOVA conducts an F - test to determine whether variation in Y is due to varying levels of X.
- ANOVA is used to test for significance of regression:
- \(H_0\): population slope coefficient \(\beta_1\) \(=\) 0
- \(H_A\): population slope coefficient \(\beta_1\) \(\neq\) 0
- R reports the p-value (Significant F).
- Rejecting \(H_0\) indicates that X explains variation in Y.

The Simple Linear Regression Model
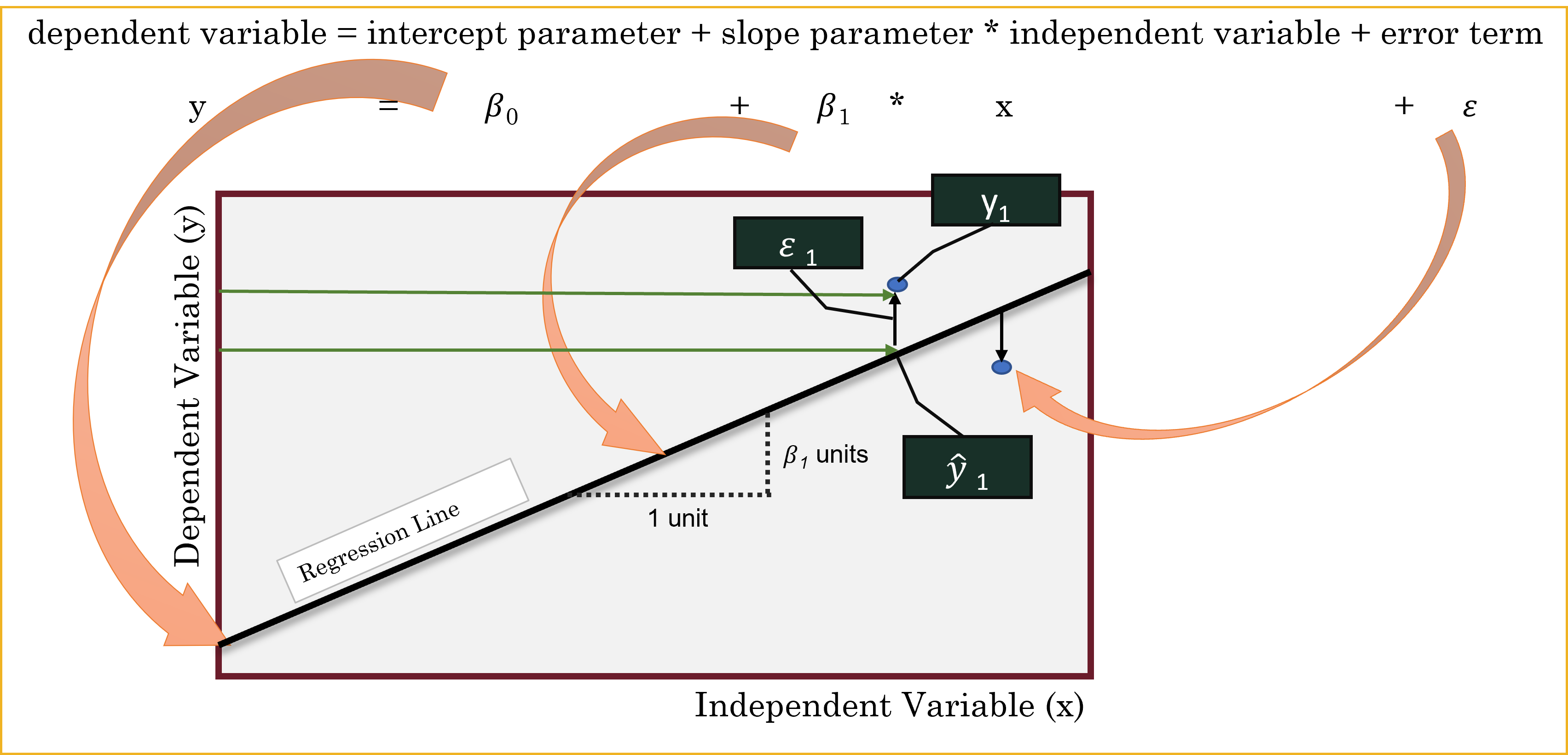
- The simple linear regression model is defined as \(y= \beta_0+\beta_1 𝑥+\varepsilon_1\), where \(y\) and \(x\) are the response and explanatory variables, respectively and \(\varepsilon_1\) is the random error term. \(\beta_0\) and \(\beta_1\) are the unknown parameters to be estimated.
- By fitting our data to the model, we obtain the equation \(\hat{y} = b_0 + b_1*x\), where \(\hat{y}\) is the estimated response variable, \(b_0\) is the estimate of \(\beta_0\) (Intercept) and \(b_1\) is the estimate of \(\beta_1\) (Slope).
- Sometimes, this equation can be represented using different variable names like \(y=mx+b\) This is the same equation as above, but different notation.
- Since the predictions cannot be totally accurate, the difference between the predicted and actual value represents the residual \(e=y-\hat{y}\).
The Least Squares Estimates
- The two parameters \(\beta_0\) and \(\beta_1\) are estimated by minimizing the sum of squared residuals.
- The slope coefficient \(\beta_1\) is estimated as \(b_1 = \sum(x_i-\bar{x}*y_i-\bar{y})/\sum(x_i-\bar{x})^2\)
- The intercept parameter \(\beta_0\) is estimated as \(b_0 = \hat{y}-b_1*\bar{x}\)
- And we use this information to make the regression equation given the formula above: \(\hat{y} = b_0 + b_1*x\),
Goodness of Fit
- Goodness of fit refers to how well the data fit the regression line. I will introduce three measures to judge how well the sample regression fits the data.
- Standard Error of the Estimate
- The Coefficient of Determination (\(R^2\))
- The Adjusted \(R^2\)
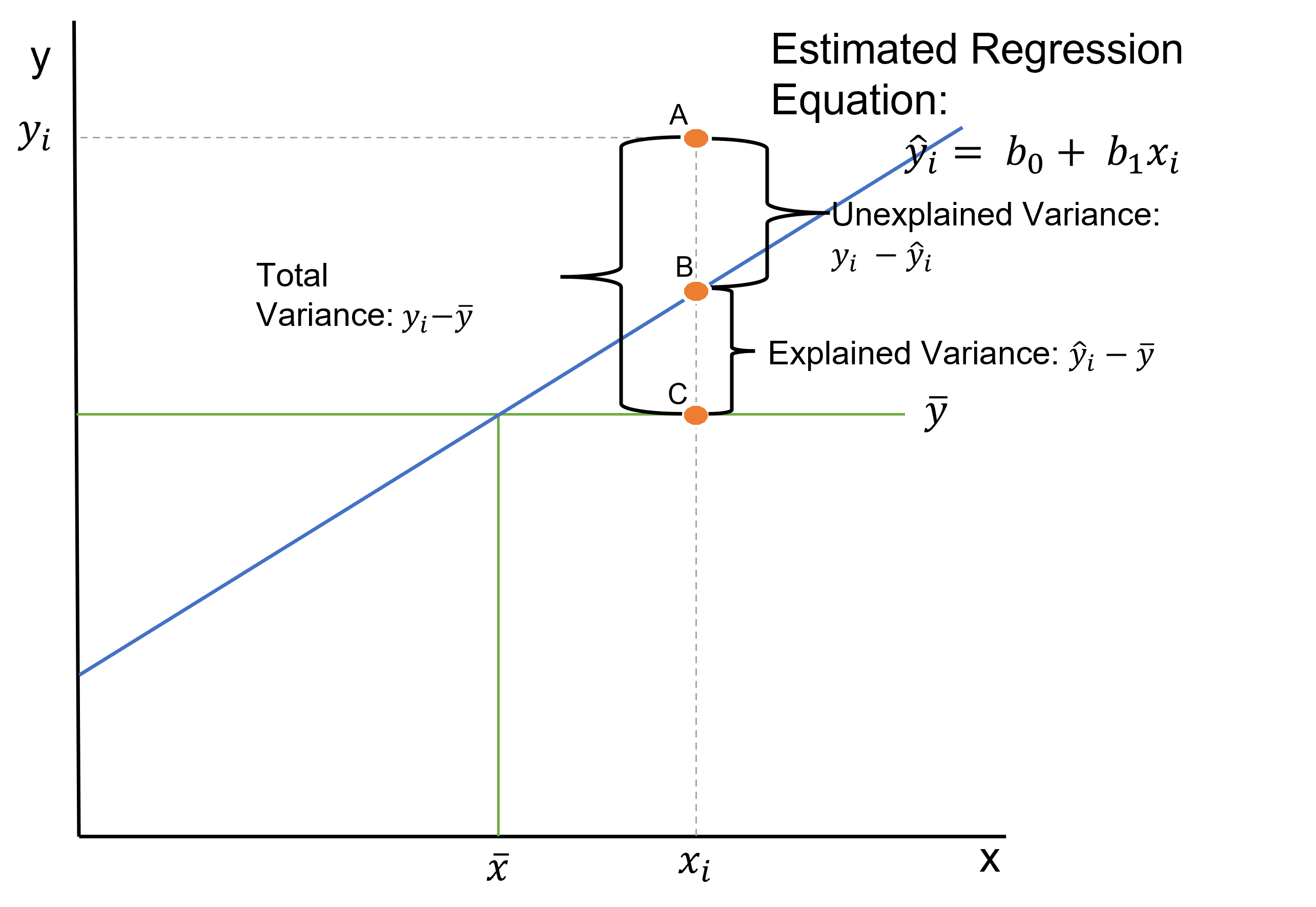
- In order to make sense of the goodness of fit measures, we need to go back to the idea of explained and unexplained variance we learned in the ANOVA lesson. Variance can also be known as a difference.
- Unexplained Variance = SSE or Sum of Squares Error: This equals the sum of squared difference between A and B, or between the sum of squares of the difference between observation (\(y_i\)) and our predicted value of y (\(\hat{y}\)).
- \(SSE = \sum^n_{i=1}(y_i - \hat{y})^2\)
- Explained Variance = SSR or Sum of Squares Regression: This equals the sum of squared difference between B and C, or between the sum of squares of the difference between our predicted value (\(\hat{y}\)) and the mean of y (\(\bar{y}\)).
- \(SSR = \sum^n_{i=1}(\hat{y} - \bar{y})^2\)
- Total Variance = SST or Total Sum of Squares: This equals the sum of squared difference between A and C, or between the sum of squares of the difference between observation (\(y_i\)) and the mean of y (\(\bar{y}\)).
- The SST can be broken down into two components: the variation explained by the regression equation (the regression sum of squares or SSR) and the unexplained variation (the error sum of squares or SSE).
- \(SST = \sum^n_{i=1}(y_i - \bar{y})^2\)
The Standard Error of the Estimate
- The Standard Error of the Estimate, also known as the Residual Standard Error (RSE) (and labelled such in R), is the variability between observed (\(y_i\)) and predicted (\(\hat{y}\)) values, targeting the unexplained variance in the figure above. This measure is a lack of fit of the model to the data.
- To compute the standard error of the estimate, we first compute the SSE and the MSE.
- Sum of Squares Error: \(SSE = \sum^n_{i=1}e^2_i = \sum^n_{i=1}(y_i - \hat{y})^2\)
- Dividing SSE by the appropriate degrees of freedom, n – k – 1, yields the mean squared error:
- Mean Squared Error: \(MSE = SSE/(n-k-1)\)
- The square root of the MSE is the standard error of the estimate, se.
- Standard Error of Estimate: \(se = \sqrt(MSE) = \sqrt(SSE/(n-k-1))\)
The Coefficient of Determination (\(R^2\))
Coefficient of determination refers to the percentage of variance in one variable that is accounted for by another variable or by a group of variables.
This measure of R-squared is a measure of the “fit” of the line to the data.
The Coefficient of Determination, denoted as \(R^2\), is a statistical measure that indicates the proportion of variance in the dependent variable (\(y\)) that is explained by the independent variable(s) (x) in a regression model. It is calculated as: SSR/SST or 1-SSE/SST. *\(R^2\) ranges from 0 to 1:
- \(R^2\)=0: None of the variance in \(y\) is explained by the model.
- \(R^2\)=1: The model explains all the variance in y. A higher \(R^2\) indicates a better fit of the model to the data.
\(R^2\) = 1-SSE/SST where \(SSE = \sum^n_{i=1}(y_i - \hat{y})^2\) and \(SST = \sum^n_{i=1}(y_i - \bar{y})^2\)
- \(R^2\) can also be computed by SSR/SST, which provides the same answer as above.
- This measure of fit targets both the unexplained and the explained variance.
- \(R^2\) can also be calculated using the formula for Pearson’s r and squaring it. This gives us the same answer.
Pearson’s \(r\) is a statistic that indicates the strength and direction of the relationship between two numeric variables that meet certain assumptions.
- (Pearson’s \(r\))\(^2\) = \(r^2_{xy} = (cov_{xy}/(s_x*s_y))^2\).
You need to see how all these formulas relate to see why all these formulas give you the same answer.
Interpreting (\(R^2\))
- This measure is easier to interpret over standard error. In particular, the (\(R^2\)) quantifies the fraction of variation in the response variable that is explained by changes in the explanatory variables.
- The (\(R^2\)) gives you a score between 0 and 1. A score of 1 indicates that your Y variable is perfectly explained by your X variable or variables (where we only have one in simple regression).
- The \(R^2\) measure has strength of determination like the correlation coefficient, only all measures are from 0 to 1.
- The closer you get to one, the more explained variance we achieve.
- A score of 0 indicates that no variance is explained by the X variable or variables. In this case, the variable would not be a significant predictor variable of Y.
- Again, the strength of the relationship varies by field, but generally, a .2 to a .5 is considered weak, a .5 to a .8 is considered moderate, and above a .8 is considered strong.
R Output
- We do see the \(R^2\) in our R output labelled Multiple R-squared.
Limitations of The Coefficient of Determination (\(R^2\))
- More explanatory variables always result in a higher \(R^2\).
- But some of these variables may be unimportant and should not be in the model.
- This is only applicable with multiple regression, discussed below.
The Adjusted \(R^2\)
The Adjusted Coefficient of Determination, denoted as Adjusted \(R^2\) modifies \(R^2\) to account for the number of predictors in the model relative to the number of data points. It is calculated as Adjusted \(R^2 = 1-(1-R^2)*((n-1)/(n-k-1))\), where where n is the sample size and p is the number of predictors.
In simple linear regression, \(R^2\) is generally more appropriate than Adjusted \(R^2\) because there is only one predictor variable in the model.
The Adjusted \(R^2\) tries to balance the raw explanatory power against the desire to include only important predictors.
- Adjusted \(R^2 = 1-(1-R^2)*((n-1)/(n-k-1))\).
- The Adjusted \(R^2\) penalizes the \(R^2\) for adding additional explanatory variables.
R Output
- With our other goodness-of-fit measures, we typically allow the computer to compute the Adjusted \(R^2\) using commands in R.
- Therefore, we do see the Adjusted \(R^2\) in our R output labelled Adjusted R-squared.
Example of Simple Linear Regression in R
The broad steps are the same as we used in Chapter 6 and 7 when setting up the t-tests and ANOVA hypothesis: 1. set up the hypothesis 2. compute the Test Statistic and calculate probability 3. interpret results and write a conclusion.
Step 1: Set Up the Null and Alternative Hypothesis
\(H_0\): The slope of the line is equal to zero.
\(H_A\): The slope of the line is not equal to zero.
Step 2: Compute the Test Statistic and Calculate Probability
library(tidyverse)
library(ggplot2)Debt_Payments <- read.csv("data/DebtPayments.csv")
Simple <- lm(Debt ~ Income, data = Debt_Payments)
summary(Simple)
Call:
lm(formula = Debt ~ Income, data = Debt_Payments)
Residuals:
Min 1Q Median 3Q Max
-107.087 -38.767 -5.828 50.137 101.619
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 210.298 91.339 2.302 0.0303 *
Income 10.441 1.222 8.544 9.66e-09 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 63.26 on 24 degrees of freedom
Multiple R-squared: 0.7526, Adjusted R-squared: 0.7423
F-statistic: 73 on 1 and 24 DF, p-value: 9.66e-09- Step 3: Interpret the Probability and Write a Conclusion
- We interpret the probability and write a conclusion after looking at the following:
- Goodness of Fit Measures
- The F-test statistic
- The p-value from the hypothesis
- We then can interpret the hypothesis and make the regression equation if needed to make predictions.
Examining the Goodness of Fit Measures
Like the ANOVA, we need the summary() command to see the regression output.
This output includes the following:
- Standard Error of Estimate at 63.26
- a \(R^2\) of 0.7526.
- an Adjusted \(R^2\) of 0.7423
We do not really see a difference in \(R^2\) and the Adjusted \(R^2\) because we only have a simple linear regression, which includes one X. The other thing that could create a difference between these measures is having a small sample size. A small sample size could adjust the \(R^2\) down (like it did a little here \(n=28\)). In both cases, a score around .75 indicates that we are explaining about 75% of the variance in Debt Payments, which is specifically stated as 75.26% in the \(R^2\) value.
The Standard Error of Estimate - known in R as the RSE or Residual Standard Error at 63.26.
The RSE represents the average amount by which the observed values deviate from the predicted values
The RSE has the same units as the dependent variable y, making it directly interpretable in the context of the problem.
- The scale of income is in 1000s.
- Therefore, for every 1000 dollars difference in Income we could be off on our debt payments by 63.26 dollars.
Again, most statisticians interpret the \(R^2\) and the adjusted \(R^2\) over the RSE.
Examining the F-Test Statistic
- The F-statistic is a ratio of explained information (in the numerator) to unexplained information (in the denominator). If a model explains more than it leaves unexplained, the numerator is larger and the F-statistic is greater than 1. F-statistics that are much greater than 1 are explaining much more of the variation in the outcome than they leave unexplained. Large F-statistics are more likely to be statistically significant.
- We see a F-statistic in our output with a p-value of 9.66e-09, which is less than .05. This indicates that our overall model is significant, which in simple regression means that our one X predictor variable is also significant. If this F-statistic is significant, we can interpret the hypothesis.
Examining the Hypothesis
- We see a p-value on the Income row of 9.66e-09 from a t-value. This is also significant at .05 level. This p-value is the same as the F-test statistic because we only have one X variable.
- This significance means our predictor variable does influence the Y variable and that we can reject the null hypothesis and show support for our alternative hypothesis.
- This means Income does influence Debt Payments.
Interpreting the Hypothesis
- A \(b_1\) estimate of 10.441 indicates that for 1000 dollars of Income (again our data is in 1000s), the payment of dept will increase by 10.441.
- A \(b_0\) estimate of 210.298 indicates where the regression line will start given a Y at 0.
- This gives us a regression equation at \(\hat{y} = 210.298 + 10.441*Income\)
- We can graph this regression line using the abline() command on our plot we did earlier.
- As you can see from the chart, there was no data at the Y intercept, but if I extend the chart out, it does hit the y axis at 210 like stated.
- Also from the chart, we note that for each unit of income we go to the right, we go up by 10.441 units in dept payments.
plot(Debt ~ Income, data = Debt_Payments, xlim = c(0, 120), ylim = c(0,
1350))
abline(Simple)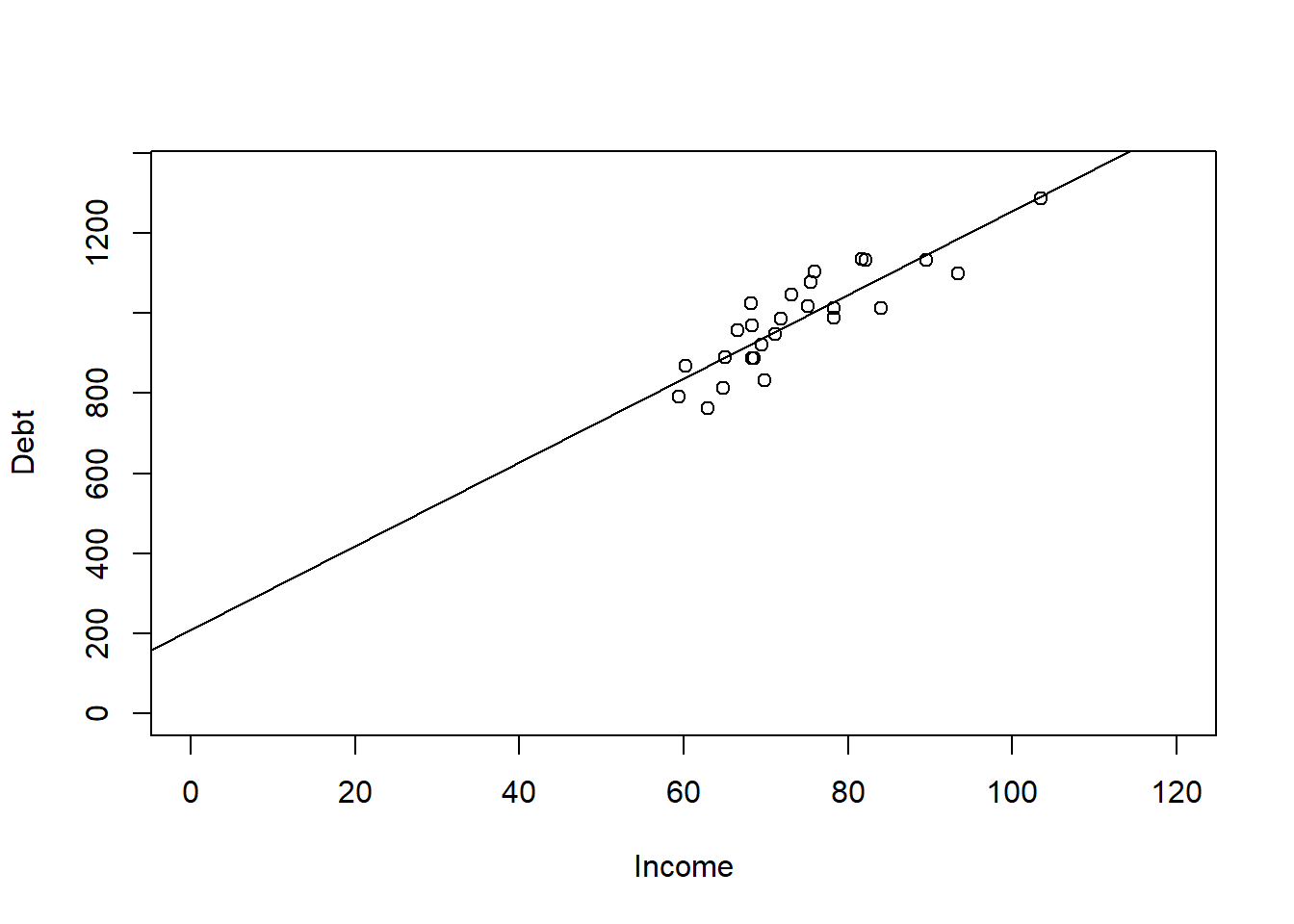
Predictions
- We can calculate this using the regression equation or use the predict() command in order to calculate different values of y given values of x based on our regression equation we got in the step above.
- The coef() function returns the model’s coefficients which are needed to make the regression equation.
# What would be your debt payments if Income was 100 ( for 100,000)
coef(Simple)(Intercept) Income
210.29768 10.44111 210.298 + 10.441 * (100)[1] 1254.398predict(Simple, data.frame(Income = 100)) 1
1254.408 Multiple Regression
Multiple regression allows us to explore how several explanatory variables influence the response variable.
Suppose there are \(k\) explanatory variables. The multiple linear regression model is defined as: \(y = \beta_0 + \beta_1x_1 + \beta_2x_2 + \ ⋯ + \beta_kx_k +\varepsilon\)
Where:
- \(y\) is the dependent variable,
- \(x_1, ⋯, x_k\) are independent explanatory variables,
- \(\beta_0\) is the intercept term,
- \(\beta_1 ⋯, \beta_k\) are the regression coefficients for the independent variables,
- \(varepsilon\) is the random error term
We estimate the regression coefficients—called partial regression coefficients — \(b_0, b_1, b_2,… b_k\), then use the model: \(\hat{y} = b_0 + b_1x_1 + b_2x_2 + \ ... + b_kx_k\) .
The partial regression coefficients represent the expected change in the dependent variable when the associated independent variable is increased by one unit while the values of all other independent variables are held constant.
For example, if there are \(k = 3\) explanatory variables, the value \(b_1\) estimates how a change in \(x_1\) will influence \(y\) assuming \(x_2\) and \(x_3\) are held constant.
Example of Multiple Linear Regression in R
- The steps to multiple linear regression are the same as simple linear regression except we should have more than one hypothesis.
- Step 1: Set up the null and alternative hypotheses
- Hypothesis 1: Income affects Debt Payments.
- \(H_0\): The slope of the line in regards to Income is equal to zero.
- \(H_A\): The slope of the line in regards to Income is not equal to zero.
- Hypothesis 2: Unemployment affects Debt Payments.
- \(H_0\): The slope of the line in regards to Unemployment is equal to zero.
- \(H_A\): The slope of the line in regards to Unemployment is not equal to zero.
- Step 2: Compute the test statistic and calculate probability
Debt_Payments <- read.csv("data/DebtPayments.csv")
Multiple <- lm(Debt ~ Income + Unemployment, data = Debt_Payments)
summary(Multiple)
Call:
lm(formula = Debt ~ Income + Unemployment, data = Debt_Payments)
Residuals:
Min 1Q Median 3Q Max
-110.456 -38.454 -5.836 51.156 102.121
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 198.9956 156.3619 1.273 0.216
Income 10.5122 1.4765 7.120 2.98e-07 ***
Unemployment 0.6186 6.8679 0.090 0.929
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 64.61 on 23 degrees of freedom
Multiple R-squared: 0.7527, Adjusted R-squared: 0.7312
F-statistic: 35 on 2 and 23 DF, p-value: 1.054e-07- Step 3: Interpret the probability and write a conclusion
- We interpret the probability and write a conclusion after looking at the following:
- Goodness of Fit Measures
- The F-test statistic
- The p-values from the hypotheses
- We then can interpret the hypotheses and make the regression equation if needed to make predictions.
Examining the Goodness of Fit Measures
- Like the ANOVA, we need the summary() command to see the regression output.
- This output includes the following:
- Standard error of estimate at 64.61 - was previously 63.26 with simple regression.
- a \(R^2\) of 0.7527 - was previously 0.7526 with simple regression.
- an Adjusted \(R^2\) of 0.7312 - was previously 0.7423 with simple regression.
- Looking at the goodness of fit indices, they suggest that we are not explaining anything more by adding the unemployment variable over what we had with the Income variable. Our RSE and \(R^2\) are about the same, and our adjusted \(R^2\) has gone down - again paying the price for including an unnecessary variable.
Examining the F-Test Statistic
- We see a overall F-statistic in our output with a p-value of 1.054e-07, which is less than .05. This indicates that our overall model is significant - which in multiple regression means that at least one X predictor variable is significant. If this F-statistic is significant, we can interpret the hypotheses.
Examining the Hypotheses
- Hypothesis 1: The output shows a p-value on the Income row of 2.98e-07 from a t-value. This was significant in our simple regression model, and is still significant at .05 level here. This significance means our predictor variable does influence the Y variable and that we can reject the null hypothesis and show support for our alternative hypothesis.
- Hypothesis 2: The output shows a p-value on the Unemployment row of 0.929 from a t-value. This is NOT significant at any appropriate level of alpha. This lack of significance means our predictor variable does NOT influence the Y variable and that we fail to reject the null hypothesis that there is a slope.
Interpreting the Hypothesis
- Because Unemployment is not significant, we should drop it from the model before creating the regression equation. The extra variable is only adding noise to our model and not adding anything useful in understanding debt payments.
The P-value Method
When you have a lot of predictors, it can be difficult to come up with a good model.
A common criteria is to remove based on the highest p-value.
Remove indicators until all variables are significant, and none are insignificant.
As we drop variables, we also want to keep an eye on the adjusted R-Squared to make sure it does not significantly decrease. It should stay about the same if we drop variables that are not helpful in understanding the model, and could improve because we are decreasing the number of variables being evaluated.
library(ISLR)
data("Credit")
str(Credit)'data.frame': 400 obs. of 12 variables:
$ ID : int 1 2 3 4 5 6 7 8 9 10 ...
$ Income : num 14.9 106 104.6 148.9 55.9 ...
$ Limit : int 3606 6645 7075 9504 4897 8047 3388 7114 3300 6819 ...
$ Rating : int 283 483 514 681 357 569 259 512 266 491 ...
$ Cards : int 2 3 4 3 2 4 2 2 5 3 ...
$ Age : int 34 82 71 36 68 77 37 87 66 41 ...
$ Education: int 11 15 11 11 16 10 12 9 13 19 ...
$ Gender : Factor w/ 2 levels " Male","Female": 1 2 1 2 1 1 2 1 2 2 ...
$ Student : Factor w/ 2 levels "No","Yes": 1 2 1 1 1 1 1 1 1 2 ...
$ Married : Factor w/ 2 levels "No","Yes": 2 2 1 1 2 1 1 1 1 2 ...
$ Ethnicity: Factor w/ 3 levels "African American",..: 3 2 2 2 3 3 1 2 3 1 ...
$ Balance : int 333 903 580 964 331 1151 203 872 279 1350 ...library(tidyverse)
## Removing variables that are of no interest to the model based on
## what we have learned so far. The following lines removes the
## categorical variables, Gender, Student, Married, and Ethnicity. It
## also removed the ID because that is not a helpful variable.
Credit <- select(Credit, -Gender, -Student, -Married, -Ethnicity, -ID)
creditlm <- lm(Balance ~ ., data = Credit)
summary(creditlm)
Call:
lm(formula = Balance ~ ., data = Credit)
Residuals:
Min 1Q Median 3Q Max
-227.25 -113.15 -42.06 45.82 542.97
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -477.95809 55.06529 -8.680 < 2e-16 ***
Income -7.55804 0.38237 -19.766 < 2e-16 ***
Limit 0.12585 0.05304 2.373 0.01813 *
Rating 2.06310 0.79426 2.598 0.00974 **
Cards 11.59156 7.06670 1.640 0.10174
Age -0.89240 0.47808 -1.867 0.06270 .
Education 1.99828 2.59979 0.769 0.44257
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 161.6 on 393 degrees of freedom
Multiple R-squared: 0.8782, Adjusted R-squared: 0.8764
F-statistic: 472.5 on 6 and 393 DF, p-value: < 2.2e-16# Multiple R-squared: 0.8782, Adjusted R-squared: 0.8764- Education has the highest p-value, so it is removed from analysis. We use the minus sign to remove the variable in the lm function.
creditlm <- lm(Balance ~ . - Education, data = Credit)
summary(creditlm)
Call:
lm(formula = Balance ~ . - Education, data = Credit)
Residuals:
Min 1Q Median 3Q Max
-231.37 -113.46 -39.55 41.66 544.35
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -449.36101 40.57409 -11.075 <2e-16 ***
Income -7.56211 0.38214 -19.789 <2e-16 ***
Limit 0.12855 0.05289 2.430 0.0155 *
Rating 2.02240 0.79208 2.553 0.0110 *
Cards 11.55272 7.06285 1.636 0.1027
Age -0.88832 0.47781 -1.859 0.0638 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 161.6 on 394 degrees of freedom
Multiple R-squared: 0.8781, Adjusted R-squared: 0.8765
F-statistic: 567.4 on 5 and 394 DF, p-value: < 2.2e-16# Multiple R-squared: 0.8781, Adjusted R-squared: 0.8765- Cards has the next highest p-value, so it is removed from analysis using the - minus sign format.
creditlm <- lm(Balance ~ . - Education - Cards, data = Credit)
summary(creditlm)
Call:
lm(formula = Balance ~ . - Education - Cards, data = Credit)
Residuals:
Min 1Q Median 3Q Max
-249.62 -110.89 -39.98 51.87 546.52
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -445.10477 40.57635 -10.970 < 2e-16 ***
Income -7.61268 0.38169 -19.945 < 2e-16 ***
Limit 0.08183 0.04461 1.834 0.0674 .
Rating 2.73142 0.66435 4.111 4.79e-05 ***
Age -0.85612 0.47841 -1.789 0.0743 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 161.9 on 395 degrees of freedom
Multiple R-squared: 0.8772, Adjusted R-squared: 0.876
F-statistic: 705.6 on 4 and 395 DF, p-value: < 2.2e-16# Multiple R-squared: 0.8772, Adjusted R-squared: 0.876- Age is next to be removed because it has the next highest p-value at .06270.
creditlm <- lm(Balance ~ . - Education - Cards - Age, data = Credit)
summary(creditlm)
Call:
lm(formula = Balance ~ . - Education - Cards - Age, data = Credit)
Residuals:
Min 1Q Median 3Q Max
-260.93 -113.14 -36.27 49.35 554.23
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -489.72748 32.09892 -15.257 < 2e-16 ***
Income -7.71931 0.37806 -20.418 < 2e-16 ***
Limit 0.08467 0.04471 1.894 0.059 .
Rating 2.69858 0.66594 4.052 6.11e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 162.4 on 396 degrees of freedom
Multiple R-squared: 0.8762, Adjusted R-squared: 0.8753
F-statistic: 934.6 on 3 and 396 DF, p-value: < 2.2e-16# Multiple R-squared: 0.8762, Adjusted R-squared: 0.8753Finally Limit is the next to be removed because it has the next highest (and still insignificant) p-value at .059.
Age is next to be removed because it has the next highest p-value at .06270.
creditlm <- lm(Balance ~ . - Education - Cards - Age - Limit, data = Credit)
summary(creditlm)
Call:
lm(formula = Balance ~ . - Education - Cards - Age - Limit, data = Credit)
Residuals:
Min 1Q Median 3Q Max
-278.57 -112.69 -36.21 57.92 575.24
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -534.81215 21.60270 -24.76 <2e-16 ***
Income -7.67212 0.37846 -20.27 <2e-16 ***
Rating 3.94926 0.08621 45.81 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 162.9 on 397 degrees of freedom
Multiple R-squared: 0.8751, Adjusted R-squared: 0.8745
F-statistic: 1391 on 2 and 397 DF, p-value: < 2.2e-16# Multiple R-squared: 0.8751,Adjusted R-squared: 0.8745- In our original model with non-helpful insignificant predictors, we had an adjusted R-Squared at 0.8764. After removing insignificant predictors, we are only down to .8745. This means we can explain someones Balance best by understanding Income and Rating.
- The interpretation is as follows:
- A one unit change in Income causes a negative 7.67 change in Balance.
- A one unit change in Rating causes a 3.949 change in Balance.
Multicollinerity
- Multicollinearity refers to the situation in which two or more predictor variables are closely related to another.
- Collinearity can cause significant factors to be insignificant, or insignificant factors to seem significant. Both are problematic.
- If sample correlation coefficient between 2 explanatory variables is more than .80 or less than -.80, we could have severe multicollinearity. Seemingly wrong signs of estimated regression coefficients may also indicate multicollinearity. A good remedy may be to simply drop one of the collinear variables if we can justify it as redundant.
- Alternatively, we could try to increase our sample size.
- Another option would be to try to transform our variables so that they are no longer collinear.
- Last, especially if we are interested only in maintaining a high predictive power, it may make sense to do nothing.
cor(Credit$Income, Credit$Rating) ##close to .8, but still under[1] 0.7913776- The second way to tell if there is multicollinearity is to use the vif() command from the car package.
- The vif() function in R is used to calculate the Variance Inflation Factor (VIF) for each predictor variable in a multiple regression model. The VIF quantifies how much the variance of a regression coefficient is inflated due to multicollinearity among the predictors. High VIF values indicate high multicollinearity, which can affect the stability and interpretability of the regression coefficients.
- We want all scores to be under 10 to indicate the absence of problematic multicollinerity in our model.
library(car) ##need to have car package installed first.
# Place regression model object in the function to see vif scores.
vif(creditlm) Income Rating
2.67579 2.67579 - While statisticians differ on what constitutes, the general consensus is that scores need to be under 5 or 10.
- Both scores are under 10, so we do have an absence of multicollinerity in our final model.
- VIF = 1: No correlation between the predictor and the other predictors.
- 1 < VIF < 5: Moderate correlation but not severe enough to require correction. Scores less than 5 pass assumption.
- 5 < VIF < 10: High correlation, indicating potential multicollinearity problems. We keep an eye on this issue, but pass the assumption.
- VIF >= 10: High correlation, indicating multicollinearity problems. Fail assumption.
Regression with Categorical Variables
Simple and multiple regression both require a continuous dependent variable (y). However, the predictor variables (x) can be categorical or continuous. If you were to have a y/x pairing with a continuous y and a categorical x, you might as well choose to run an ANOVA from the last module or a t-test if there are only 2 categories. However, if you have a more complex model, or need to try a variety of models, multiple regression allows for you to seamlessly add and delete predictor variables (both categorical and continuous).
We often have categorical predictors in modeling settings. And it might not make sense to think about a “one unit increase” in a categorical variable. In regression settings, we can account for categorical variables by creating dummy variables, which are indicator variables for certain conditions happening. When considering categorical variables, one variable is taken to be the baseline or reference value. All other categories will be compared to it.
Regression analysis requires numerical data.
Ordinal variables can be represented by a number in one column when there is even distance between the categories.
- From strongly disagree to disagree to N/A to agree to strongly agree. Each 1 unit change considers the same distance between points.
- A weighted scale would go from strongly disagree to neither to agree to strongly agree to agree all the time.
- Need to manually code these and coerce into a number.
- Some ordinal variables need to use dummy coding in R (i.e., Seasonality). Need to always check rationale before blindly recoding to numbers, or using numbers that were provided.
Nominal categorical data can be included as independent variables, but must be coded numeric using dummy variables.
- R will create the dummy variables automatically in a regression using the lm() command.
- For variables with 2 categories, code as 0 and 1.
Dummy Variables with More than 2 Categories
- Like in an ANOVA test, a categorical variable may be defined by more than two categories.
- Use multiple dummy variables to capture all categories, one for each category.
- When a categorical variable has k > 2 levels, we need to add k − 1 additional variables to the model.
- Given the intercept term, we exclude one of the dummy variables from the regression.
- The excluded variable represents the reference category.
- Including all dummy variables creates perfect multicollinearity (which is an assumption discussed in your textbook).
- Example: mode of transportation with three categories
- Public transportation, driving alone, or car pooling
- \(d_1=1\) for public transportation and 0 otherwise
- \(d_2=1\) for driving alone and 0 otherwise
- \(d_1=d_2=0\) indicates car pooling
- Public transportation, driving alone, or car pooling
- Slope estimates of categorical data cannot be evaluated the same way. In the example below, since Gender is nominal, and because we are using regression, we should use dummy variables to process this factor in the regression instead of the method above. We can use this technique for ordinal variables to recode them into numeric. Again, R does this coding on our behalf using the lm() command.
# Take a vector representing gender
gender <- c("MALE", "FEMALE", "FEMALE", "UNKNOWN", "MALE")
# One way is to convert the data into numerical in the column using
# ifelse statements.
ifelse(gender == "MALE", 1, ifelse(gender == "FEMALE", 2, 99))[1] 1 2 2 99 1Example Using Dummy Variables
- Suppose that we are forecasting and we want to account for the month as a predictor.
- Then the following dummy variables can be created the following way:
sales <- read.csv("data/months.csv", stringsAsFactors = TRUE)
str(sales)'data.frame': 132 obs. of 3 variables:
$ Month: Factor w/ 12 levels "Apr","Aug","Dec",..: 1 2 3 4 5 6 7 8 9 10 ...
$ Year : int 2010 2010 2010 2010 2010 2010 2010 2010 2010 2010 ...
$ Units: int 45420 44558 63844 39338 35000 45747 50923 46786 48696 55000 ...library(tidyverse)ggplot(sales, aes(x = Month, y = Units)) + geom_boxplot()
- I produced a boxplot of the monthly data across units above. April (Apr) is the first month listed (not Jan for January). It alphabetizes it from there from left to right.
- Looking at the lm() command summary below, the hypotheses take on the format VariableCategory. So MonthAug corresponds to the Month variable with the Aug category, representing August. You will notice that there is no MonthApr listed. It is considered the referent category and held in the intercept.
- The interpretation of each of the coefficients associated with the dummy variables is that it is a measure of the effect of that category relative to the omitted or referent category.
- In the example to the left, the intercept coefficient is associated with April, so MonthAug measures the effect of August on the forecast variable (Units) compared to the effect of April.
- Since the data represents the difference in Units sold in months, we can interpret the predicted units sold for April as 49,580.8.
- August was significantly different than April because there is a p-value less than .05. Specifically, we can expect about 7701.6 more units to be sold in August over April. December, January, June, and November also had significantly different Units sold.
- February, July, March, May, October, and September are not different than April because the p-value is > .05.
- Never try to remove a categorical variable that is not significant because it means something else - that the category is not different than the referent category. More on this later.
# Suppose that we are forecasting daily data and we want to account
# for the month as a predictor. Then the following dummy variables
# can be created.
lmSales <- lm(Units ~ Month, data = sales)
summary(lmSales)
Call:
lm(formula = Units ~ Month, data = sales)
Residuals:
Min 1Q Median 3Q Max
-12724.5 -4056.6 -36.3 3620.9 22066.5
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 49580.8 1749.6 28.339 < 2e-16 ***
MonthAug 7701.6 2474.2 3.113 0.00232 **
MonthDec 25245.7 2474.2 10.203 < 2e-16 ***
MonthFeb -3744.7 2474.2 -1.513 0.13279
MonthJan -6939.5 2474.2 -2.805 0.00588 **
MonthJul 1809.8 2474.2 0.731 0.46592
MonthJun 4971.5 2474.2 2.009 0.04675 *
MonthMar 3671.9 2474.2 1.484 0.14042
MonthMay 3652.1 2474.2 1.476 0.14255
MonthNov 14205.6 2474.2 5.741 7.21e-08 ***
MonthOct -125.4 2474.2 -0.051 0.95967
MonthSep 261.8 2474.2 0.106 0.91590
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 5803 on 120 degrees of freedom
Multiple R-squared: 0.6857, Adjusted R-squared: 0.6569
F-statistic: 23.8 on 11 and 120 DF, p-value: < 2.2e-16# The Intercept absorbs the referent category and so in this case,
# April is alphabetically first and the referent category.- We can reset the levels by using the factor() command. Shown below, I reset the levels of the month in order from month 1 (Jan) to month 12 (Dec). This puts “Jan” in the referent category when we rerun the regression. This allows us to compare Jan to other months and to specifically, test what months are different from Jan (+ increase in sales from Jan, - a decrease in sales from Jan).
- For example, March has 10612 more unit sales than Jan. If not significant, like MonthFeb, then you can interpret as not significantly different than the 42K in Jan.
sales$Month <- factor(sales$Month, levels = c("Jan", "Feb", "Mar", "Apr",
"May", "Jun", "Jul", "Aug", "Sep", "Oct", "Nov", "Dec"))
ggplot(sales, aes(x = Month, y = Units)) + geom_boxplot()
lmSales <- lm(Units ~ Month, data = sales)
summary(lmSales)
Call:
lm(formula = Units ~ Month, data = sales)
Residuals:
Min 1Q Median 3Q Max
-12724.5 -4056.6 -36.3 3620.9 22066.5
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 42641 1750 24.373 < 2e-16 ***
MonthFeb 3195 2474 1.291 0.199106
MonthMar 10612 2474 4.289 3.65e-05 ***
MonthApr 6940 2474 2.805 0.005877 **
MonthMay 10592 2474 4.281 3.77e-05 ***
MonthJun 11911 2474 4.814 4.36e-06 ***
MonthJul 8749 2474 3.536 0.000578 ***
MonthAug 14641 2474 5.917 3.17e-08 ***
MonthSep 7201 2474 2.911 0.004302 **
MonthOct 6814 2474 2.754 0.006803 **
MonthNov 21145 2474 8.546 4.78e-14 ***
MonthDec 32185 2474 13.008 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 5803 on 120 degrees of freedom
Multiple R-squared: 0.6857, Adjusted R-squared: 0.6569
F-statistic: 23.8 on 11 and 120 DF, p-value: < 2.2e-16# The interpretation of each of the coefficients associated with the
# dummy variables is that it is a measure of the effect of that
# category relative to the omitted category. In the example to the
# left, the intercept coefficient is associated with January, so
# MonthFeb measures the effect of Feb on the forecast variable
# (Units) compared to the effect of Jan.Example Using a Continuous and Categorical Variable
- Let’s do an example with the GNP.csv data set to use GNP and quarterly data to predict Sales (in millions)
GNP <- read.csv("data/GNP.csv")
str(GNP)'data.frame': 40 obs. of 4 variables:
$ Year : int 2007 2007 2007 2007 2008 2008 2008 2008 2009 2009 ...
$ Quarter: int 1 2 3 4 1 2 3 4 1 2 ...
$ Sales : int 921266 1013371 1000151 1060394 950268 1028016 999824 957207 828677 905562 ...
$ GNP : num 14302 14513 14718 14880 14849 ...# #1, 2, 3, 4 represent the quarter and we want that data as
# categorical
GNP$Quarter <- as.factor(GNP$Quarter)
# #Evaluate Quarterly data of GNP in a boxplot.
GNP %>%
ggplot(aes(x = Quarter, y = Sales)) + geom_boxplot()
# Run the linear regression considering GNP and Quarterly data
lmGNP <- lm(Sales ~ GNP + Quarter, data = GNP)
summary(lmGNP)
Call:
lm(formula = Sales ~ GNP + Quarter, data = GNP)
Residuals:
Min 1Q Median 3Q Max
-53748 -20083 -700 16341 52626
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -61669.572 52583.805 -1.173 0.249
GNP 65.055 3.215 20.234 < 2e-16 ***
Quarter2 78278.963 13576.443 5.766 1.57e-06 ***
Quarter3 59960.212 13607.096 4.407 9.49e-05 ***
Quarter4 108765.258 13638.197 7.975 2.21e-09 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 30330 on 35 degrees of freedom
Multiple R-squared: 0.9364, Adjusted R-squared: 0.9291
F-statistic: 128.7 on 4 and 35 DF, p-value: < 2.2e-16# Estimate y, where y and x are Sales and GNP, and 2 is a quarter 2
# dummy, 3 is a Quarter 3 dummy, and 4 is a Quarter 4 dummy.
# All else equal, retail sales in quarter 1 are expected to be
# approximately $108,765 million less than sales in quarter 4.
# What are the predicted sales in quarter 2 if GNP is $18,000 (in
# billions)?
Quarter2 <- 18000
coef(lmGNP) (Intercept) GNP Quarter2 Quarter3 Quarter4
-61669.57208 65.05476 78278.96330 59960.21187 108765.25801 # Using the equation
-61669.57208 + 65.05476 * Quarter2 + 78278.963[1] 1187595# When you use the predict() command with a categorical variable, you
# need to include the predictors with what they equal as shown below.
# I pulled out the data.frame() command into a new variable named nd
# to simplify our predict() command later on.
nd <- data.frame(GNP = 18000, Quarter = "2")
predict(lmGNP, nd) 1
1187595 # You can write the above 2 lines like shown below for the same
# answer.
predict(lmGNP, data.frame(GNP = 18000, Quarter = "2")) 1
1187595 - While you technically can keep adding categorical variables, you must be careful not to add too many because the intercept becomes increasingly difficult to interpret!
Coffee Example
Visualizing
- Let’s try a bigger example with the coffee dataset.
library(tidyverse)
library(ggplot2)
library(dplyr)
coffee <- read.csv("data/coffee.csv", stringsAsFactors = TRUE)
str(coffee)'data.frame': 1311 obs. of 31 variables:
$ X : int 1 2 3 4 5 6 7 8 9 10 ...
$ Species : Factor w/ 1 level "Arabica": 1 1 1 1 1 1 1 1 1 1 ...
$ Owner : Factor w/ 306 levels "","acacia hills ltd",..: 206 206 125 302 206 154 137 95 95 75 ...
$ Country.of.Origin : Factor w/ 37 levels "","Brazil","Burundi",..: 10 10 11 10 10 2 26 10 10 10 ...
$ Farm.Name : Factor w/ 558 levels "","-","1","200 farms",..: 374 374 441 526 374 1 1 19 19 510 ...
$ ICO.Number : Factor w/ 843 levels "","-","??","0",..: 455 455 1 1 455 1 1 98 98 454 ...
$ Company : Factor w/ 271 levels "","ac la laja sa de cv",..: 169 169 1 264 169 1 208 1 1 88 ...
$ Number.of.Bags : int 300 300 5 320 300 100 100 300 300 50 ...
$ Bag.Weight : Factor w/ 56 levels "0 kg","0 lbs",..: 47 47 3 47 47 32 51 47 47 47 ...
$ Harvest.Year : Factor w/ 47 levels "","08/09 crop",..: 16 16 1 16 16 14 13 41 41 16 ...
$ Processing.Method : Factor w/ 6 levels "","Natural / Dry",..: 6 6 1 2 6 2 6 1 1 2 ...
$ Color : Factor w/ 5 levels "","Blue-Green",..: 4 4 1 4 4 3 3 1 1 4 ...
$ Aroma : num 8.67 8.75 8.42 8.17 8.25 8.58 8.42 8.25 8.67 8.08 ...
$ Flavor : num 8.83 8.67 8.5 8.58 8.5 8.42 8.5 8.33 8.67 8.58 ...
$ Aftertaste : num 8.67 8.5 8.42 8.42 8.25 8.42 8.33 8.5 8.58 8.5 ...
$ Acidity : num 8.75 8.58 8.42 8.42 8.5 8.5 8.5 8.42 8.42 8.5 ...
$ Body : num 8.5 8.42 8.33 8.5 8.42 8.25 8.25 8.33 8.33 7.67 ...
$ Balance : num 8.42 8.42 8.42 8.25 8.33 8.33 8.25 8.5 8.42 8.42 ...
$ Uniformity : num 10 10 10 10 10 10 10 10 9.33 10 ...
$ Clean.Cup : num 10 10 10 10 10 10 10 10 10 10 ...
$ Sweetness : num 10 10 10 10 10 10 10 9.33 9.33 10 ...
$ Cupper.Points : num 8.75 8.58 9.25 8.67 8.58 8.33 8.5 9 8.67 8.5 ...
$ Moisture : num 0.12 0.12 0 0.11 0.12 0.11 0.11 0.03 0.03 0.1 ...
$ Category.One.Defects: int 0 0 0 0 0 0 0 0 0 0 ...
$ Quakers : int 0 0 0 0 0 0 0 0 0 0 ...
$ Category.Two.Defects: int 0 1 0 2 2 1 0 0 0 4 ...
$ unit_of_measurement : Factor w/ 2 levels "ft","m": 2 2 2 2 2 2 2 2 2 2 ...
$ altitude_low_meters : num 1950 1950 1600 1800 1950 ...
$ altitude_high_meters: num 2200 2200 1800 2200 2200 NA NA 1700 1700 1850 ...
$ altitude_mean_meters: num 2075 2075 1700 2000 2075 ...
$ TotalScore : num 90.6 89.9 89.8 89 88.8 ...- Sometimes, we are only interested in 2 or 3 category values. In the following example, I am filtering by Processing Method and creating a ggplot only holding the methods of interest to me.
coffee %>%
filter(Processing.Method == "Natural / Dry" | Processing.Method ==
"Washed / Wet" | Processing.Method == "Other") %>%
ggplot(aes(x = Processing.Method, y = TotalScore)) + geom_boxplot(color = rainbow(3))
- Does not look like large group differences, good indication into what we will find.
- In the next visualization, lets add in a scatterplot to show the difference between 2 continuous variables (Flavor and TotalScore) using Processing Method method as the color.
coffee %>%
filter(Processing.Method == "Natural / Dry" | Processing.Method ==
"Washed / Wet" | Processing.Method == "Other") %>%
ggplot(aes(x = Flavor, y = TotalScore, color = Processing.Method)) +
geom_point(aes(fill = Processing.Method))
- In the chart above, flavor almost looks like a perfect predictor, strong and positive.
2 Categories
- Suppose there are only 2 processing methods for coffee beans: Wet/Washed and Natural/Dry.
R takes Natural/Dry as the referent category value. Then we can create one dummy variable. A Dummy Variable is then assigned as either a 0 or 1. Let’s save the filtering of 2 methods into a new smaller dataset first and then running the lm model.
coffee2cat <- filter(coffee, Processing.Method == "Natural / Dry" | Processing.Method ==
"Washed / Wet")
head(coffee2cat$Processing.Method)[1] Washed / Wet Washed / Wet Natural / Dry Washed / Wet Natural / Dry
[6] Washed / Wet
6 Levels: Natural / Dry Other ... Washed / Wet- Next, lets run a lm model using the newly filtered data.
lmModel <- lm(TotalScore ~ Processing.Method, data = coffee2cat)
summary(lmModel)
Call:
lm(formula = TotalScore ~ Processing.Method, data = coffee2cat)
Residuals:
Min 1Q Median 3Q Max
-22.1346 -0.9944 0.4554 1.5354 8.6154
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 82.3541 0.1704 483.193 <2e-16 ***
Processing.MethodWashed / Wet -0.3895 0.1950 -1.997 0.046 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.7 on 1061 degrees of freedom
Multiple R-squared: 0.003746, Adjusted R-squared: 0.002807
F-statistic: 3.99 on 1 and 1061 DF, p-value: 0.04603- We can make a prediction of Washed/Wet.
predict(lmModel, data.frame(Processing.Method = "Washed / Wet")) 1
81.96462 coef(lmModel) (Intercept) Processing.MethodWashed / Wet
82.3541434 -0.3895252 82.3541 - 0.3895[1] 81.9646Using More Than 2 Categories
A categorical variable may be defined by more than two categories.
Like mentioned above, we use multiple dummy variables to capture all categories, one for each category.
When a categorical variable has k > 2 levels, we need to add k − 1 additional variables to the model.
Given the intercept term, we exclude one of the dummy variables from the regression.
The excluded variable represents the reference category. Example: Processing.Time Filtering by 3 categories: “Natural / Dry” “Washed / Wet“ or Other”) \(d_1=1\) for Other and 0 otherwise \(d_2=1\) for Washed/Wet and 0 otherwise \(d_1=d_2=0\) indicates Natural/Dry referent category
\(Score_i=β_0+β_1(I(Other)_i)+β_2(I(Wet)_i)+ϵ_I\) \(β_0\) represents the expected score for a coffee with 0 for the two dummy variables. That is, if it was a dry process coffee \(β_1\) represents the expected difference in score for coffee with an Other roasting process, compared to the baseline level (dry process) \(β_2\) represents the expected difference in score for Washed/Wet process coffee compared to dry process coffee. We have to estimate multiple “slopes” for this one variable - one corresponding to each non-reference level.
We can refilter the data to include the third category value.
coffee3cat <- filter(coffee, Processing.Method == "Natural / Dry" | Processing.Method ==
"Washed / Wet" | Processing.Method == "Other")
head(coffee3cat) X Species Owner Country.of.Origin
1 1 Arabica metad plc Ethiopia
2 2 Arabica metad plc Ethiopia
3 4 Arabica yidnekachew dabessa Ethiopia
4 5 Arabica metad plc Ethiopia
5 6 Arabica ji-ae ahn Brazil
6 7 Arabica hugo valdivia Peru
Farm.Name ICO.Number
1 metad plc 2014/2015
2 metad plc 2014/2015
3 yidnekachew dabessa coffee plantation
4 metad plc 2014/2015
5
6
Company Number.of.Bags Bag.Weight Harvest.Year
1 metad agricultural developmet plc 300 60 kg 2014
2 metad agricultural developmet plc 300 60 kg 2014
3 yidnekachew debessa coffee plantation 320 60 kg 2014
4 metad agricultural developmet plc 300 60 kg 2014
5 100 30 kg 2013
6 richmond investment-coffee department 100 69 kg 2012
Processing.Method Color Aroma Flavor Aftertaste Acidity Body Balance
1 Washed / Wet Green 8.67 8.83 8.67 8.75 8.50 8.42
2 Washed / Wet Green 8.75 8.67 8.50 8.58 8.42 8.42
3 Natural / Dry Green 8.17 8.58 8.42 8.42 8.50 8.25
4 Washed / Wet Green 8.25 8.50 8.25 8.50 8.42 8.33
5 Natural / Dry Bluish-Green 8.58 8.42 8.42 8.50 8.25 8.33
6 Washed / Wet Bluish-Green 8.42 8.50 8.33 8.50 8.25 8.25
Uniformity Clean.Cup Sweetness Cupper.Points Moisture Category.One.Defects
1 10 10 10 8.75 0.12 0
2 10 10 10 8.58 0.12 0
3 10 10 10 8.67 0.11 0
4 10 10 10 8.58 0.12 0
5 10 10 10 8.33 0.11 0
6 10 10 10 8.50 0.11 0
Quakers Category.Two.Defects unit_of_measurement altitude_low_meters
1 0 0 m 1950
2 0 1 m 1950
3 0 2 m 1800
4 0 2 m 1950
5 0 1 m NA
6 0 0 m NA
altitude_high_meters altitude_mean_meters TotalScore
1 2200 2075 90.58
2 2200 2075 89.92
3 2200 2000 89.00
4 2200 2075 88.83
5 NA NA 88.83
6 NA NA 88.75- We can make our new model object with the lm function.
lmModel2 <- lm(TotalScore ~ Processing.Method, data = coffee3cat)
summary(lmModel2)
Call:
lm(formula = TotalScore ~ Processing.Method, data = coffee3cat)
Residuals:
Min 1Q Median 3Q Max
-22.1346 -0.9646 0.4554 1.5354 8.6154
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 82.3541 0.1728 476.694 <2e-16 ***
Processing.MethodOther -1.0757 0.5639 -1.908 0.0567 .
Processing.MethodWashed / Wet -0.3895 0.1977 -1.971 0.0490 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.737 on 1086 degrees of freedom
Multiple R-squared: 0.005435, Adjusted R-squared: 0.003603
F-statistic: 2.967 on 2 and 1086 DF, p-value: 0.05186- The overall model is not significant here, but one group still shows differences. Means poor predictor, but that there are still group differences (even if small) between Washed/Wet and Natural/Dry
- Finally, we can make our new prediction of what the score would be in the Processing.Method was Other.
predict(lmModel2, data.frame(Processing.Method = "Other")) 1
81.27846 coef(lmModel2) (Intercept) Processing.MethodOther
82.3541434 -1.0756819
Processing.MethodWashed / Wet
-0.3895252 82.3541434 - 1.0756819[1] 81.27846Adding in a Numerical Variable
- We can add in another variable like Flavor. Flavor is a much stronger predictor.
lmModel3 <- lm(TotalScore ~ Flavor + Processing.Method, data = coffee3cat)
summary(lmModel3)
Call:
lm(formula = TotalScore ~ Flavor + Processing.Method, data = coffee3cat)
Residuals:
Min 1Q Median 3Q Max
-16.6648 -0.3555 0.2157 0.7248 5.7972
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 31.4116 1.0691 29.380 < 2e-16 ***
Flavor 6.7151 0.1403 47.849 < 2e-16 ***
Processing.MethodOther -0.1274 0.3205 -0.398 0.69108
Processing.MethodWashed / Wet 0.2931 0.1130 2.593 0.00964 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.553 on 1085 degrees of freedom
Multiple R-squared: 0.6802, Adjusted R-squared: 0.6793
F-statistic: 769.3 on 3 and 1085 DF, p-value: < 2.2e-16predict(lmModel3, data.frame(Flavor = 10, Processing.Method = "Other")) 1
98.43565 coef(lmModel3) (Intercept) Flavor
31.4116160 6.7151441
Processing.MethodOther Processing.MethodWashed / Wet
-0.1274019 0.2931262 31.411616 + 6.7151441 * 10 + -0.1274019[1] 98.43566- After adjusting for aroma, and flavor, is there sufficient evidence to suggest a difference in mean score between dry vs. wet process beans? Explain, using a formal hypothesis test. $H_0: Processing.Method_{Washed / Wet} = Processing.Method_{Dry} $ $H_A: Processing.Method_{Washed / Wet}Processing.Method_{Dry} $
lmModel4 <- lm(TotalScore ~ Aroma + Flavor + Processing.Method, data = coffee2cat)
summary(lmModel4)
Call:
lm(formula = TotalScore ~ Aroma + Flavor + Processing.Method,
data = coffee2cat)
Residuals:
Min 1Q Median 3Q Max
-17.5344 -0.2720 0.2208 0.7122 4.7629
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 28.1650 1.1482 24.530 < 2e-16 ***
Aroma 1.6013 0.2134 7.502 1.32e-13 ***
Flavor 5.5406 0.1987 27.884 < 2e-16 ***
Processing.MethodWashed / Wet 0.2337 0.1079 2.166 0.0306 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.479 on 1059 degrees of freedom
Multiple R-squared: 0.7017, Adjusted R-squared: 0.7009
F-statistic: 830.6 on 3 and 1059 DF, p-value: < 2.2e-16We find evidence that there is a difference between Washed/Wet processed coffee beans and dry processed beans as evident by the significant p-value < .05.
Adjusting for aroma, flavor, and process, which country has the highest expected score? The lowest?
## calculate the predicted scores in the dataset
predicted_scores <- predict(lmModel4, newdata = coffee2cat)
# Create a new dataframe with Country and predicted scores
predicted_data <- data.frame(Country = coffee2cat$Country, Predicted_Score = predicted_scores)
# Find the country with the highest expected score
highest_expected_score <- filter(predicted_data, Predicted_Score == max(Predicted_Score))
highest_expected_score Country Predicted_Score
1 Ethiopia 91.20569# Find the country with the lowest expected score
lowest_expected_score <- filter(predicted_data, Predicted_Score == min(Predicted_Score))
lowest_expected_score Country Predicted_Score
990 Guatemala 73.56705We find that Ethiopia has the highest predicted score and Guatemala has the lowest predicted score based on Aroma, Flavor, and Processing Method.
What percentage of the variability in the total score is explained by a linear relationship with the predictors in your model?
library(broom)
glance(lmModel4)# A tibble: 1 × 12
r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 0.702 0.701 1.48 831. 1.35e-277 3 -1922. 3854. 3879.
# ℹ 3 more variables: deviance <dbl>, df.residual <int>, nobs <int>- We can look at the R-squared value of .693 and adjusted R-squared value of .692 and state that about 69% of the variable in total score is explained by a linear relationship with the predictors in our model.
Using AI
Use the following prompts on a generative AI, like chatGPT, to learn more about regression analysis in R.
Explain the difference between covariance and correlation. How do you interpret the direction and strength of a correlation coefficient?”
What is covariance, and how does it describe the relationship between two variables? Provide an example with a simple dataset. Describe Pearson’s correlation coefficient. How do you calculate it, and what does it tell you about the relationship between two variables?
Explain how to create a scatterplot using ggplot2 in R to visualize the relationship between two continuous variables. How can you add a regression line to assess the linearity of the relationship?
How can you use the cor.test() function in R to conduct a hypothesis test for correlation? What do the p-value and confidence interval indicate in the context of correlation?
How do you interpret the strength and direction of a correlation? What is considered a strong, moderate, or weak correlation in the context of business data?
Explain the null and alternative hypotheses for correlation testing. How does the t-distribution play a role in testing the significance of a correlation coefficient?
What are some challenges of visualizing relationships between variables when dealing with big data, and how can statistical tests help when scatterplots are not effective?
Discuss the limitations of correlation analysis. Why is it important to be cautious when interpreting correlation as causation?
What are the key differences between correlation and causation? How can you determine if a correlation implies causality?
Explain how to perform simple linear regression in R. Use the lm() function and discuss how to interpret the slope, intercept, and R-squared values from the regression output.
What is the coefficient of determination (R-squared) in regression analysis, and how does it relate to the goodness of fit? How can the residual standard error (RSE) and adjusted R-squared help in interpreting a model?
Describe how to perform multiple linear regression in R using the lm() function. How do you interpret the coefficients for multiple predictors, and what do the p-values tell you about their significance?
What does the F-statistic in a regression output indicate? How does it help in determining the significance of a regression model, and what role does it play when comparing multiple models?
Explain how ANOVA is related to regression analysis. How can the F-test be used to assess the significance of regression models? What are residuals in a regression model, and how can analyzing them help assess model fit? How is the sum of squared errors (SSE) related to residual analysis?
What is multicollinearity, and why is it problematic in multiple regression? How can you detect multicollinearity in R using the vif() function, and what steps can be taken to address it?
How can you use a fitted regression model to make predictions for new data in R? Explain how the predict() function works and provide an example using both simple and multiple regression.
Given the output from the summary() function for a regression model in R, explain how to interpret the coefficients, R-squared, adjusted R-squared, residual standard error, and p-values.
Describe how to use the p-value method for variable selection in multiple regression. How do you iteratively remove insignificant predictors while monitoring the R-squared and adjusted R-squared values?
Summary
- In this lesson, we explored the correlation coefficient, learning how to evaluate the strength and direction of a correlation (strong, moderate, weak; positive or negative) and how to visualize relationships using scatterplots. We also learned to test whether a correlation is statistically significant. Additionally, we delved into simple and multiple linear regression models, understanding how to write and interpret these models, assess goodness-of-fit measures, and test hypotheses by interpreting the summary output from the lm() command. Finally, we examined how regression can incorporate both continuous and categorical predictor variables.