# Below is written in plain english pseudocode
SET total to 0
FOR each element in the list
ADD element to total
RETURN totalAlgorithm Design and Pseudocode
Automate This by Christopher Steiner
An algorithm is a set of operations (mathematical, technical) to be conducted in a certain sequence to achieve a certain goal.
This book discusses the rise of algorithms and their transformative impact on industries.
- Algorithms have gone from being a tool used by a few specialists to becoming a driving force in business, finance, healthcare, and more.
- Automation through algorithms is reshaping the world, with both positive and negative implications.
Algorithms Key Concepts and Examples
- Algorithms in Finance: High-Frequency Trading (HFT) revolutionized Wall Street by executing trades at lightning speeds, leading to both massive profits and new risks.
- Algorithms in Healthcare: Algorithms that diagnose diseases faster and more accurately than doctors.
- Music: Algorithms used by platforms like Pandora to predict and recommend songs.
- Impact on Jobs: Automation’s role in replacing jobs traditionally done by humans, particularly in industries like finance, journalism, and even art.
Future Implications and Ethical Considerations
- Expansion of Algorithms: The growing reach of algorithms in decision-making processes, from hiring practices to legal judgments.
- Ethical Concerns: The potential for bias in algorithms and the importance of transparency in their design. The need for regulation and oversight as algorithms increasingly influence critical aspects of life.
- Looking Ahead: Steiner’s call for society to adapt to the new algorithm-driven world, balancing innovation with ethical responsibility.
Bias in Algorithms Explored
- Facial Recognition Technology algorithms have shown significant biases, particularly in accurately identifying people of different races and genders.
- Studies have found that some facial recognition systems have higher error rates when identifying individuals with darker skin tones and women. This can lead to discriminatory outcomes, such as misidentifying people of color at higher rates than white individuals.
- Impact: This bias can result in wrongful accusations or the exclusion of certain groups from services that rely on facial recognition technology.
- Hiring algorithms are used by companies to screen job applicants, but they can unintentionally perpetuate biases present in the training data.
- A famous case involved an AI hiring tool developed by Amazon, which was found to be biased against female applicants. The algorithm was trained on resumes submitted over the previous decade, which were predominantly from male applicants, leading the AI to favor male candidates.
- Impact: This bias can reinforce gender inequalities in the workplace by systematically disadvantaging qualified female applicants.
- Predictive Policing algorithms analyze historical crime data to predict where future crimes are likely to occur, influencing law enforcement patrols.
- These algorithms often reflect existing biases in policing practices, such as disproportionately targeting minority neighborhoods. Because the training data may contain biased policing patterns, the algorithm can perpetuate over-policing in certain communities.
- Impact: This can lead to a cycle of increased surveillance and criminalization of specific racial or ethnic groups, reinforcing systemic biases in the criminal justice system.
How to Design an Algorithm:
- A Routing Problem: Find a good path from Williamsburg to Los Angeles
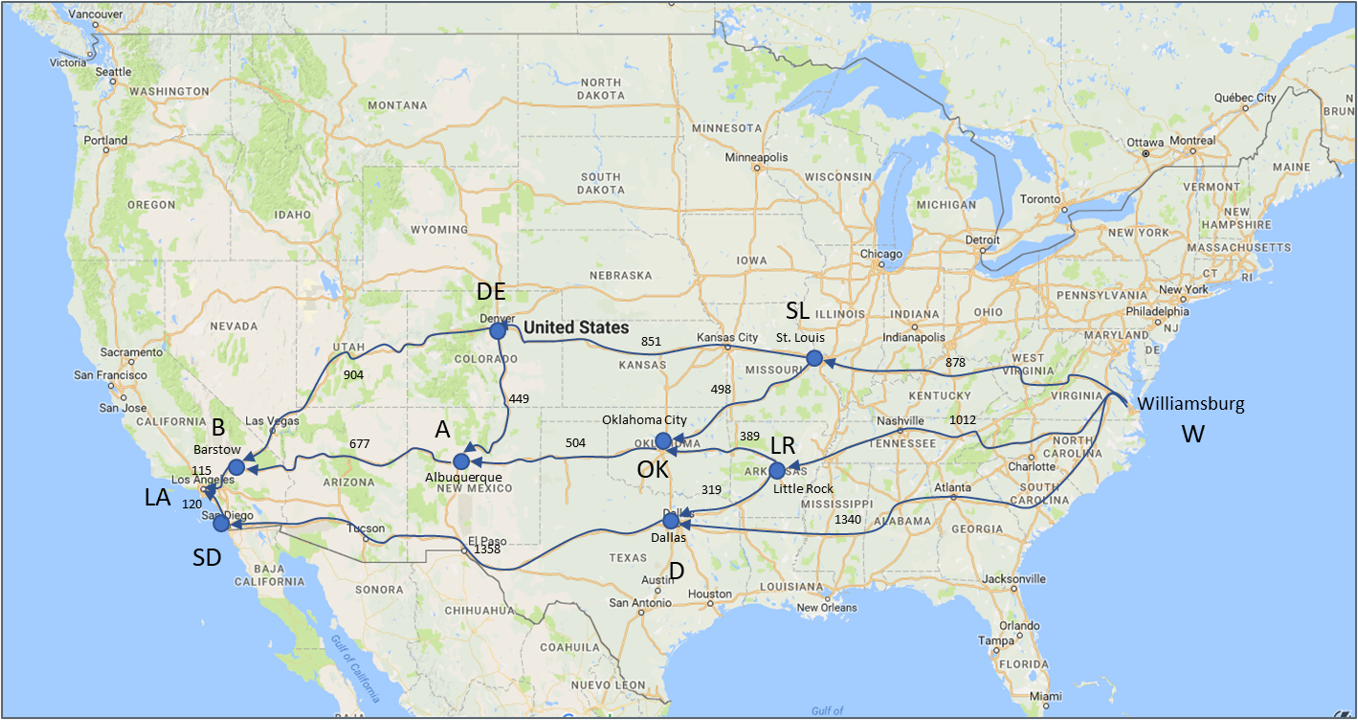
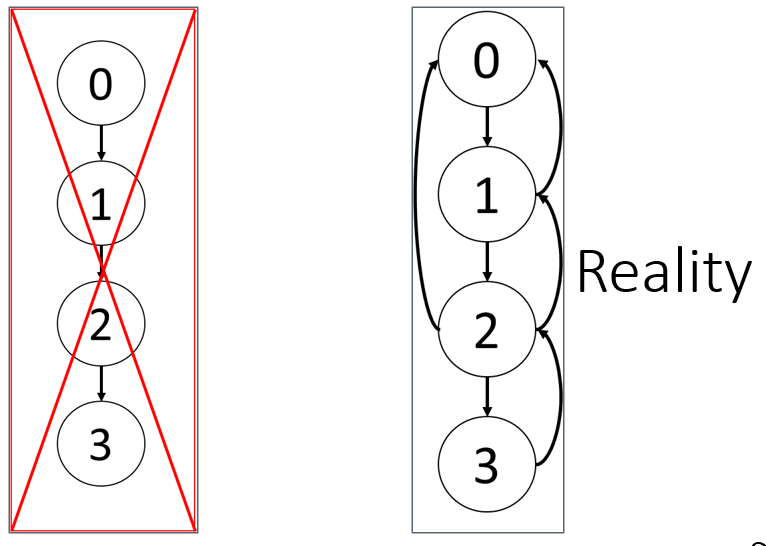
Algorithm Development Process:
What should you do first?
0: Think of a conceptual approach
- AI can help clarify the problem or suggest high-level strategies
- You must decide what the algorithm is trying to achieve and why
1: Step-by-step outline (AI-assisted)
- AI can help draft pseudocode or outlines
- You should verify logical flow and constraints
2: Implementation planning (AI-accelerated)
- AI can suggest:
- Data structures
- Loop patterns
- Function decomposition
- You evaluate trade-offs: speed, memory, readability
- AI can suggest:
3: Coding & debugging (AI as pair programmer)
- AI can:
- Generate boilerplate code
- Help interpret error messages
- You must:
- Test incrementally
- Validate correctness
- Ensure alignment with the original logic
- AI can:
Understanding the Structure of Algorithms
- Identify the Purpose:
- Start by understanding what the algorithm is supposed to achieve.
- Look for a brief description or goal at the beginning.
- Break Down the Steps:
- Algorithms are typically presented as a sequence of steps.
- Each step corresponds to a specific action or decision.
- in words. Focus on sound logic.
- Recognize Input and Output:
- Determine what inputs the algorithm requires.
- Identify the expected output(s) after the algorithm is executed.
How to Write Pseudocode
- Define the problem:
- Start by clearly understanding what the algorithm should do.
- Break the problem into steps:
- Write the steps in logical order.
- Think in terms of inputs, processing, and outputs.
- Use simple control structures:
- IF, ELSE, FOR, WHILE are commonly used.
- Clearly show decision points and iterations.
- Be clear and concise:
- Avoid unnecessary details (e.g., language-specific syntax).
- Focus on the algorithm’s logic rather than code specifics.
- Test your pseudocode:
- Mentally trace through the steps to ensure they make sense.
- Make sure it covers all cases (e.g., edge cases, conditions)
- AI can help draft pseudocode, but you are responsible for validating the logic.
Pseudocode Know-how
Don’t include code-specific features such as variable declarations, data types, or specific keywords.
Focus on what the algorithm should do, not how to implement it.
Use pseudocode to outline the flow and logic of the solution.
Think of pseudocode as a blueprint that can be implemented in any programming language
Bad: int sum = 0; for (i=0; i < n; i++) sum += arr[i];
Good:
# Below the pseudocode is written more code like (also correct):
SET sum = 0
FOR each element in the list
sum = sum + number
RETURN sumTips for Writing Good Pseudocode
- Maintain consistent terms throughout: Use the same terminology for variables, functions, and processes. If you define a variable as total, always refer to it as total, not sum later on.
- Be clear on naming: Use descriptive names for variables, functions, and operations to make your pseudocode intuitive.
- Pseudocode should be easy to understand after a single read-through. If it feels too complex, break it down further.
Examples of Pseudocode
- This pseudocode below calculates the sum of all numbers in the list that are greater than a specified threshold by iterating through the list and adding qualifying numbers to the sum.
- edge cases: an empty list, all even numbers, or no numbers greater than the threshold.
# Pseudocode for summing numbers greater than a given threshold
SET sum = 0
FOR each number IN list:
IF number > threshold:
SET sum = sum + number
RETURN sum- This pseudocode finds the smallest number in a given list by iterating through all elements and updating the min_number whenever a smaller number is found.
# Pseudocode for finding the minimum number in a list
SET min_number = Infinity
FOR each number IN list:
IF number < min_number:
SET min_number = number
RETURN min_numberBasic TSP Formulation (Optimization)
Objective Function: \[ \text{Minimize} \quad Z = \sum_{i=1}^{n} \sum_{j=1, j \neq i}^{n} c_{ij} x_{ij} \]
- Explanation: This formula represents the objective function of the TSP, where \(c_{ij}\) is the cost (or distance) of traveling from city \(i\) to city \(j\), and \(x_{ij}\) is a binary variable that equals 1 if the path from \(i\) to \(j\) is included in the solution and 0 otherwise. The goal is to minimize the total travel cost.
Constraints:
\(\sum_{j=1, j \neq i}^{n} x_{ij} = 1 \quad \forall i\)
\(\sum_{i=1, i \neq j}^{n} x_{ij} = 1 \quad \forall j\)
\(x_{ij} \in \{0, 1\}\)
- Explanation: The first constraint ensures that each city \(i\) is exited exactly once, and the second constraint ensures that each city \(j\) is entered exactly once. The binary constraint on \(x_{ij}\) ensures that the solution only includes valid paths.
TSP Nearest Neighbor Algorithm (Heuristic):
\(Z = \sum_{i=1}^{n-1} c_{i, \text{NN}(i)} + c_{n, \text{NN}(1)}\)
- Explanation: This is the cost calculation for the nearest neighbor heuristic, where \(\text{NN}(i)\) denotes the nearest neighbor of city \(i\). The tour starts at a city, repeatedly visits the nearest unvisited city, and returns to the starting city.
Code-Like Pseudocode for TSP Nearest Neighbor Model (Heuristic)
- Nearest Neighbor Heuristic: The algorithm works by greedily choosing the nearest unvisited city until all cities are visited, then returning to the start city.
- Output: It outputs the route and the total distance traveled.
### inputs
SET cities = <list of cities>
SET distances = <distance matrix or dictionary>
SET start_city = <initial city>
### FUNCTION to find the nearest unvisited city
FUNCTION find_nearest_neighbor(current_city, unvisited, distances):
SET nearest_city = None
SET min_distance = infinity
FOR each city IN unvisited:
IF distances[current_city][city] < min_distance:
SET min_distance = distances[current_city][city]
SET nearest_city = city
RETURN nearest_city, min_distance
### FUNCTION to solve TSP using Nearest Neighbor algorithm
FUNCTION nearest_neighbor_tsp(start_city, cities, distances):
# Initialize list of unvisited cities
SET unvisited = list of all cities EXCEPT start_city
# Set starting point
SET current_city = start_city
SET route = [start_city]
SET total_distance = 0
# Visit all cities
WHILE unvisited is NOT empty:
SET next_city, distance = find_nearest_neighbor(current_city, unvisited, distances)
ADD next_city to route
INCREASE total_distance by distance
SET current_city = next_city
REMOVE next_city from unvisited
# Return to the starting city to complete the tour
INCREASE total_distance by distances[current_city][start_city]
ADD start_city to route
RETURN route, total_distance
### Run the TSP algorithm
SET route, total_distance = nearest_neighbor_tsp(start_city, cities, distances)
### Output the result
PRINT "Route using Nearest Neighbor heuristic:", route
PRINT "Total distance traveled:", total_distanceTranslate Pseudocode into Code:
- Determine how the algorithm progresses through its steps and notice the flow control structures like loops (for, while) and conditionals (if, else).
- How to we increase the ease of coding and development?
- Begin to consider speed, memory usage, convenience tradeoffs
- Identify variables and understand their roles (e.g., counters, accumulators).
- Which data types should we use?
- Which fields for dictionary labels?
- How should lists be sorted, if at all?
- Should we use a for or while loop?
- Should we use functions?
- Program in chunks
- Test each chunk before moving on
- Use functions where reasonable
- Functions are easier to test
- Check code where solutions are known
- Small problems
- Obvious solutions
- Debug often
- Create breakpoints where needed
- Check variables in console
- Add print statements
Deciphering Algorithmic Notation
- Pay attention to the data types being used (e.g., integers, strings, lists, dictionaries). Note that the operations you need matter more than how the data looks.
- Lists
- Best when you will iterate through the entire collection
- Ordered and mutable
- Common Methods: sort, reverse, append
- Ideal when values may change or be reordered
- Tuples
- Similar to lists, but used when the data shouldn’t change
- Immutable
- Fewer built-in methods
- Useful for fixed records (e.g., coordinates)
- Dictionaries
- Best for fast random access using a key Keys must be unique
- Slightly more overhead than lists
- Ideal when data has meaningful labels (key-value pairs)
Deciphering Algorithmic Notation: Mathematical Symbols
- Mathematical Symbols:
- Algorithms often include mathematical notation, such as sums (\(\sum\)) or products (\(\prod\)).
- Understand these as they relate to the algorithm’s operations.
- Big-O Notation:
- Look for references to Big-O notation, which indicates the algorithm’s efficiency in terms of time or space.
- Understand the implications for performance, especially with large inputs.
- Commenting
- Commenting improves code readability, reuse, and maintainability.
- Can transfer algorithm outline to a program as comments.
- Then, you have comments that provide an outline for coding.
Calculating Wall Time
- Wall time refers to the real-world time that elapses from the start to the end of a process or block of code.
- time.time(): Returns the current time in seconds since the epoch (January 1, 1970). This uses the time module. When running, save it to a start_time variable.
import time
start_time = time.time()- Execute the block of code you want to measure and end the time.
end_time = time.time()- Subtract the start time from the end time to get the elapsed wall time and then print the elapsed time.
elapsed_time = end_time - start_time
print(f"Wall time: {elapsed_time:.2f} seconds")Wall time: 0.02 secondsWriting Programs with Internal Functions
- Indentation: Function statements must be indented
- Arguments: Variables passed from calling program to the function
- a_list is an argument required by my_sum
- a_list assumes value of x passed from main
- a_list is an argument required by my_sum
- Return: a return statement sends variables back to main program
- Variable scope: where execution begins
- The first unindented line that is not a function definition or a global variable
- a_list is defined only in the function when it runs
- Place all functions above the “main” program
- Must be defined before they are used
def my_sum(a_list):
result = 0
for y in a_list:
result += y
return result
x = [0,1,2,3,4,5]
print(my_sum(x))15## 15Understanding The Loop
- A loop is a way to repeat the same action for every item in a collection (like a list).
- For y in a_list means, take each item in a_list one at a time, and call it y.
for y in a_list:
result += y
return result- For example, if a_list is [0, 1, 2, 3, 4, 5], the loop will do the following:
- First loop: set y = 0, result = 0 + 0 (result is now 0).
- Second loop: Then, set y = 1, result = 0 + 1 (result is now 1).
- Third loop: then y = 2, result = 1 + 2 (result is now 3).
- and so on, until all the numbers in the list have been used.
- First loop: set y = 0, result = 0 + 0 (result is now 0).
The Return Statement Inside Functions
- You need a RETURN statement when an algorithm or function is expected to produce an output that will be used later.
- If something needs to come back out of the algorithm, use RETURN. * For example:
- Evaluation functions need RETURN (score, cost, fitness)
- Move / neighbor functions often return a new solution
- Search loops may return best solution found
- You DO need RETURN when:
- The algorithm computes a value (sum, average, best solution, prediction)
- The result will be stored, printed, or passed to another step
- You are writing a function (not just a sequence of actions)
- The algorithm’s purpose is to output a value, so a return is needed
SET total to 0 FOR each element in the list ADD element to total RETURN total
- You DO NOT need RETURN when:
- The algorithm only performs actions
- Results are displayed, saved, or modify something in place
- You are describing a procedure, not a function
- Nothing is handed back for later use.
FOR each student PRINT student name
Using AI
Use the following prompt on a generative AI, like chatGPT, to learn more about the topics covered.
Defining Algorithms: Explain, in your own words, what an algorithm is and provide an example from everyday life (e.g., a recipe or a set of instructions).
Ethics and Bias: Discuss one example of algorithmic bias, such as facial recognition or hiring algorithms. What could be done to address these biases?
Routing Problem: Given a problem like finding the shortest path from point A to point B, outline a step-by-step algorithm using pseudocode.
Flow Control: Illustrate how flow control structures (e.g., loops and conditionals) help manage decision-making in algorithms. Provide a simple example in pseudocode.
Optimization Considerations: Discuss how tradeoffs between speed, memory usage, and convenience influence algorithm design. Can you think of a scenario where one must be prioritized over others?
Pseudocode to Code: Write a pseudocode for a basic task (e.g., calculating the average of a list of numbers) and then translate it into Python code.
Interpreting Pseudocode: Given a pseudocode example from the slides (e.g., the TSP example), explain the purpose and main steps of the algorithm.
Choosing Data Structures: Compare lists, tuples, and dictionaries in Python. Provide examples of when each would be the most appropriate choice in an algorithm.
Sorting and Searching: Write pseudocode for a simple sorting algorithm (e.g., bubble sort) and explain its time complexity in terms of Big-O notation.
TSP Complexity: Explain why the Traveling Salesman Problem (TSP) is computationally challenging. How does the Nearest Neighbor approach simplify the problem?
Algorithm Design Paradigms: Compare heuristic-based algorithms to optimization-based approaches. When might a heuristic be preferred over an exact method?
Debugging Steps: What are some strategies to debug algorithms effectively during implementation? Share an experience or hypothetical scenario where one of these strategies was crucial.
Ethical Considerations in Practice: Imagine you are tasked with designing a hiring algorithm. How would you ensure it is free from bias and promotes equity?
Conclusions
- Resist the urge to start by writing code!!!
- Invest time upfront developing your approach.
- Conceptual and implementation plan.
- Invest time upfront developing your approach.
- The code writes itself if you have a good understanding of the formula and good pseudocode.
- More time now planning… a lot less time later coding.